The Hamiltonian of free particle in 2D non-Hermitian position-dependent noncommutative space reads as follows
$$\begin{aligned} {\hat{H}}_F=\frac{1}{2m_0}\left( {\hat{P}}_x^2+{\hat{P}}_y^2\right) . \end{aligned}$$
(34)
As mentioned, any Hamiltonian depending on the operators \({\hat{X}}\) or \({\hat{P}}_y\) will obviously no longer be Hermitian. Thus, using the relations (5), we can transform the Hamiltonian (34) into the standard \(\theta\)-deformed operator (2) as follows
$$\begin{aligned} {\hat{H}}_F=\frac{1}{2m_0}\left[ {\hat{p}}_{x_0}^2+\left( 1-\tau {\hat{y}}_0+\tau ^2 {\hat{y}}_0^2\right) ^2 {\hat{p}}_{y_0}^2-i\hbar \tau (1+2\tau {\hat{y}}_0)(1-\tau {\hat{y}}_0 +\tau ^2{\hat{y}}_0^2){\hat{p}}_{y_0}\right] . \end{aligned}$$
(35)
Evidently this Hamiltonian is non-Hermitian \({\hat{H}}\ne {\hat{H}}^\dag\). Thus, the Hermicity requirement of this operator is achieved by means of a similarity transformation using the Dyson map. Thus, the Hermitian counterpart Hamiltonian becomes
$$\begin{aligned} {\hat{h}}_F=\eta {\hat{H}}_F\eta ^{-1}= \frac{1}{2m_0}\left( {\hat{p}}_x^2+{\hat{p}}_y^2\right) . \end{aligned}$$
(36)
Using the relation (11,13), we rewrite the Hamiltonian in terms of the \(\theta\)-noncommutative operators
$$\begin{aligned} {\hat{h}}_F=\frac{1}{2m_0}\left[ {\hat{p}}_{x_0}^2+ (1-\tau {\hat{y}}_0 +\tau ^2 {\hat{y}}_0^2)^{1/2}{\hat{p}}_{y_0} (1-\tau {\hat{y}}_0 +\tau ^2 {\hat{y}}_0^2) {\hat{p}}_{y_0} (1-\tau {\hat{y}}_0 +\tau ^2 {\hat{y}}_0^2)^{1/2}\right] . \end{aligned}$$
(37)
Appealing to the nonsymmetric Bopp-shift (3), we may rewrite the above Hamiltonian as follows
$$\begin{aligned} {\hat{h}}_F=\frac{1}{2m_0}\left[ {\hat{p}}_{x_s}^2+ (1-\tau {\hat{y}}_s +\tau ^2 {\hat{y}}_s^2)^{1/2}{\hat{p}}_{y_s} (1-\tau {\hat{y}}_s +\tau ^2 {\hat{y}}_s^2) {\hat{p}}_{y_s} (1-\tau {\hat{y}}_s +\tau ^2 {\hat{y}}_s^2)^{1/2}\right] . \end{aligned}$$
(38)
The time-independent Schrödinger equation is given by
$$\begin{aligned} {\hat{h}}_F\psi (x_s,y_s)= & {} E\psi (x_s,y_s),\nonumber \\ ({\hat{h}}_F^x+{\hat{h}}_F^y) \psi (x_s,y_s)= & {} E\psi (x_s,y_s). \end{aligned}$$
(39)
As it is clearly seen, the system is decoupled and the solution to the eigenvalue Eq. (39) is given by
$$\begin{aligned} \psi (x_s,y_s)= \psi (x_s)\psi (y_s), \quad E=E_x+E_y \end{aligned}$$
(40)
where \(\psi (x_s)\) is the wave function in the \(x_s\)-direction and \(\psi (y_s)\) the wave function in the \(y_s\)-direction. Since the particle is free in the \(x_s\)-direction, the wave function is given by26
$$\begin{aligned} \psi _k(x_s)=\int _{-\infty }^{+\infty } dk g(k)e^{ikx_s}, \end{aligned}$$
(41)
where g(k) determines the shape of the wave packet and the energy spectrum is continuous26
$$\begin{aligned} E_x=E_k=\frac{\hbar ^2 k^2}{2m_0}. \end{aligned}$$
(42)
In \(y_s\)-direction, we have to solve the following equation
$$\begin{aligned} \frac{1}{2m_0} (1-\tau {\hat{y}}_s +\tau ^2 {\hat{y}}_s^2)^{1/2}{\hat{p}}_{y_s} (1-\tau {\hat{y}}_s +\tau ^2 {\hat{y}}_s^2) {\hat{p}}_{y_s} (1-\tau {\hat{y}}_s +\tau ^2 {\hat{y}}_s^2)^{1/2}\psi (y_s)=E_y\psi (y_s). \end{aligned}$$
(43)
This equation is an agreement with the one introduced by von Roos67 for systems with a position-dependent mass (PDM) operator and it can be rewritten as68
$$\begin{aligned} \left( -\frac{\hbar ^2}{2m_0}\root 4\, \of {\frac{m_0}{m(y_s)}}\frac{\partial }{\partial _{y_s}}\sqrt{\frac{m_0}{m(y_s)}}\frac{\partial }{\partial _{y_s}}\root 4\, \of {\frac{m_0}{m(y_s)}}\right) \psi (y_s)=E_y \psi (y_s), \end{aligned}$$
(44)
where
$$\begin{aligned} m({\hat{y}}_s)=\frac{m_0}{(1-\tau {\hat{y}}_s +\tau ^2 {\hat{y}}_s^2)^2 }, \end{aligned}$$
(45)
being the PDM of the system strongly pertubated by quantum gravity13. The PDM is illustated in Fig. 6 as a function of the position \(y_s\) \((0< y_s < 0.3)\). In this description, the effective mass of \(m({\hat{y}}_s)\) increases with \(\tau\). This indicates that quantum gravitational fields increase with \(m({\hat{y}}_s)\). Otherwise, by increasing experimentally the PDM, one can make the quantum gravitational effects stronger for a measurement through the variation of the PDM of the system. Furthermore, the increase of PDM with the quantum gravitational effect will be a consequence of the deformation of the quantum energy levels, allowing the particle to jump from one state to another with low energy Figure 8. This observation is perfectly analogous to the theory of GR in which massive objects induce strong gravitational fields and curve space, allowing the surrounding light systems to fall down with low energies..
PDM versus the position \(y_s\) for different values of \(\tau\).
The Eq. (44) can be conveniently rewritten by means of the transformation \(\psi (y_s)=\root 4\, \of {m(y_s)/m_0}\phi (y_s)\) as in68
$$\begin{aligned} -\frac{\hbar ^2}{2m_0}\left( \sqrt{\frac{m_0}{m(y_s)}}\frac{\partial }{\partial _{y_s}}\right) ^2\phi (y_s)=E_y \phi (y_s),\quad \text{ with } \quad E_y >0, \end{aligned}$$
(46)
or
$$\begin{aligned} -\frac{\hbar ^2}{2m_0}\left[ (1-\tau y_s+\tau ^2 y_s^2)^2\frac{\partial ^2}{\partial _{y_s^2}}- \tau (1-2\tau y_s)(1-\tau y_s+\tau ^2 y_s^2)\frac{\partial }{\partial _{y_s}}\right] \phi (y_s)=E_y \phi (y_s). \end{aligned}$$
(47)
The solution of this Eq. (47) is given by13
$$\begin{aligned} \phi _\lambda (y_s)= & {} A\exp \left( i\frac{2\lambda }{\tau \sqrt{3}} \left[ \arctan \left( \frac{2\tau y_s-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] \right) , \end{aligned}$$
(48)
$$\begin{aligned} \psi _\lambda (y_s)= & {} \frac{A}{\sqrt{1-\tau y_s+\tau ^2 y_s^2}}\exp \left( i\frac{2\lambda }{\tau \sqrt{3}} \left[ \arctan \left( \frac{2\tau y_s-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] \right) , \end{aligned}$$
(49)
where \(\lambda =\frac{\sqrt{2m_0E_y}}{\hbar }\) and A is the normalization constant. We notice that if the standard wave-function \(\psi _\lambda (y_s)\) is normalized, then \(\phi _\lambda (y_s)\) is normalized under a \(\tau\)-deformed integral. Indeed, we have
$$\begin{aligned} \int _{-\infty }^{+\infty } dy_s\psi _\lambda ^*(y_s)\psi _\lambda (y_s)= \int _{-\infty }^{+\infty }\frac{dy_s}{1-\tau y_s+\tau ^2 y_s^2} \phi _\lambda ^*(y_s)\phi _\lambda (y_s)=1. \end{aligned}$$
(50)
Based on this Eq. (50), the normalized constant A is determined as follows
$$\begin{aligned} 1= & {} \int _{-\infty }^{+\infty }\frac{dy_s}{1-\tau y_s+\tau ^2 y_s^2} \phi _\lambda ^*(y_s)\phi _\lambda (y_s) \end{aligned}$$
(51)
$$\begin{aligned}= & {} A^2 \int _{-\infty }^{+\infty }\frac{dy_s}{1-\tau y_s+\tau ^2 y_s^2}, \end{aligned}$$
(52)
so, we find
$$\begin{aligned} A=\sqrt{\frac{\tau \sqrt{3}}{2\pi }}. \end{aligned}$$
(53)
The next important point concerns, is the quantization of the energy spectrum; we will show below that this property comes directly from the orthogonality of these solutions. Since the operator \({\hat{h}}_y\) is Hermitian, then the corresponding eigenfunctions \(\psi _\lambda (y_s)\) are orthogonal. This property can be shown by considering the integral
$$\begin{aligned} \int _{-\infty }^{+\infty } dy_s{\hat{h}}_y^\dag \psi _{\lambda ‘}^*(y_s)\psi _{\lambda }(y_s)= \int _{-\infty }^{+\infty } dy_s{\hat{\psi }}_\lambda ^*(y_s){\hat{h}}_y\psi _\lambda (y_s), \end{aligned}$$
(54)
which becomes, after an integration by parts,
$$\begin{aligned} E_{\lambda ‘}\int _{-\infty }^{+\infty } dy_s \psi _{\lambda ‘}^*(y_s)\psi _{\lambda }(y_s)= E_{\lambda } \int _{-\infty }^{+\infty } dy_s\hat{\psi }_{\lambda ‘}^*(y_s)\psi _\lambda (y_s). \end{aligned}$$
(55)
Since these two integrals are equal, one has
$$\begin{aligned} (E_{\lambda ‘}-E_{\lambda })\int _{-\infty }^{+\infty } dy_s \psi _{\lambda ‘}^*(y_s)\psi _{\lambda }(y_s)= & {} 0, \end{aligned}$$
(56)
$$\begin{aligned} (E_{\lambda ‘}-E_{\lambda })\int _{-\infty }^{+\infty } dy_s \frac{A^2}{1-\tau y_s+\tau ^2 y_s^2}e^{i\frac{2(\lambda -\lambda ‘)}{\tau \sqrt{3}} \left[ \arctan \left( \frac{2\tau y_s-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] }= & {} 0, \end{aligned}$$
(57)
$$\begin{aligned} \sin \left( \frac{\lambda -\lambda ‘}{\tau \sqrt{3}}\pi \right)= & {} 0. \end{aligned}$$
(58)
The quantization follows from the Eq. (58) and leads to the equation
$$\begin{aligned} \frac{\lambda -\lambda ‘}{\tau \sqrt{3}}\pi= & {} n\pi \nonumber \\ \lambda -\lambda ‘= & {} \lambda _n=\tau n\sqrt{3}, \quad \quad \quad n\in {\mathbb {N}}, \end{aligned}$$
(59)
where one notices the case \(n=0\) i.e. \(\lambda =\lambda ‘\), corresponding to the normalization condition considered in (54). Then, the energy spectrum of the particle is written as
$$\begin{aligned} E_y=E_n=\frac{3\tau ^2 \hbar ^2}{2m_0}n^2. \end{aligned}$$
(60)
As it is clairly obtained, the presence of this deformed parameter \(\tau\) in \(y_s\)-direction quantized the energy of a free particle. This fact comes to confirm the fundamental property of gravity which consists of contracting and discretizing the matter.
Then, the total eigensystem is given by
$$\begin{aligned} E={\left\{ \begin{array}{ll} E_x= \frac{\hbar ^2 k^2}{2m_0},\\ E_y=\frac{3\tau ^2 \hbar ^2}{2m_0}n^2. \end{array}\right. } \end{aligned}$$
(61)
and
$$\begin{aligned} \psi (x_s,y_s)={\left\{ \begin{array}{ll} \psi _k(x_s)= \int _{-\infty }^{+\infty } dk g(k)e^{ikx_s}, \\ \psi _n(y_s)= \frac{A}{\sqrt{1-\tau y_s+\tau ^2 y_s^2}}\exp \left( i 2n \left[ \arctan \left( \frac{2\tau y_s-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] \right) . \end{array}\right. } \end{aligned}$$
(62)
Now, we consider the above free particle of mass \(m_0\) captured in a two-dimensional box of length \(0\le x_s\le a\) and heigth \(0\le y_s\le a\). The boundaries of the box are located. We impose the wave functions \(\psi (0)=0=\psi (a)\). The eigensystems in \(x_s\)-direction are given by
$$\begin{aligned} \psi _n(x_s)=\sqrt{\frac{2}{a}}\sin \left( \frac{n\pi }{a}x_s\right) , \quad E_n=n^2\frac{\pi ^2\hbar ^2}{2m_0a^2},\quad E_1=\frac{\pi ^2\hbar ^2}{2m_0a^2}. \end{aligned}$$
(63)
Taking the results (63) as a witness, we study what follows the influence of the deformed parameter \(\tau\) on the system. In \(y_s\)-direction, the solution is given by
$$\begin{aligned} \psi _k(y_s)=\frac{B}{\sqrt{1-\tau y_s+\tau ^2 y_s^2}}\exp \left( i\frac{2k}{\tau \sqrt{3}} \left[ \arctan \left( \frac{2\tau y_s-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] \right) , \end{aligned}$$
(64)
where \(k=\frac{\sqrt{2m_0E’}}{\hbar }\). Then by normalization, \(\langle \psi _k|\psi _k\rangle =1\), we have
$$\begin{aligned} 1= & {} B^2\int _{0}^{a}\frac{dy_s}{1-\tau y_s+\tau ^2 y_s^2}, \end{aligned}$$
(65)
so we find
$$\begin{aligned} B=\sqrt{\frac{\tau \sqrt{3}}{2}} \left[ \arctan \left( \frac{2\tau a-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] ^{-1/2}. \end{aligned}$$
(66)
Based on the reference8, the scalar product of the formal eigenstates is given by
$$\begin{aligned} \langle \psi _{k’}|\psi _k\rangle= & {} \frac{\tau \sqrt{3}}{2(k-k’)\left[ \arctan \left( \frac{2\tau a-1}{\sqrt{3}}\right) \right] }\sin \left( \frac{2(k-k’)\left[ \arctan \left( \frac{2\tau a-1}{\sqrt{3}}\right) \right] }{\tau \sqrt{3}}\right) . \end{aligned}$$
(67)
This relation shows that, the normalized eigenstates (64) are no longer orthogonal. However, if one tends \((k-k’)\rightarrow \infty\), these states become orthogonal
$$\begin{aligned} \lim _{(k-k’)\rightarrow \infty } \langle \psi _{k’}|\psi _{k}\rangle =0. \end{aligned}$$
(68)
These properties show that, the states \(|\psi _k\rangle\) are essentially Gaussians centered at \((k-k’)\rightarrow 0\) (see Fig. 7). This observation indicates primordial fluctuations at this scale and these fluctuations increase with the quantum gravitational effects. The states \(|\psi _k\rangle\) can be compared to the coherent states of harmonic oscillators69,70,71,72 which are known as states that mediate a smooth transition between the quantum and classical worlds. This transition is manifested by the saturation of the Heisenberg uncertainty principle \(\Delta _z q\Delta _z p=\hbar /2\). In comparison with coherent states of harmonic oscillator, the states \(|\psi _{k}\rangle\) strongly saturate the GUP (\(\Delta _{\psi _{k}} X\Delta _{\psi _{k}}P=\hbar\)) at the Planck scale and could be used to describe the transition states between the quantum world and unknown world for which the physical descriptions are out of reach.
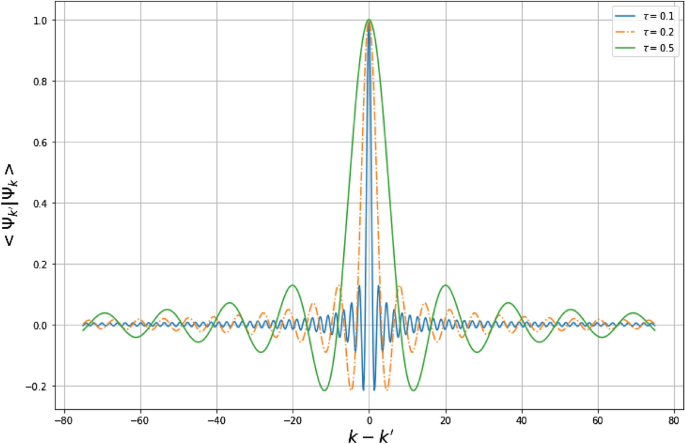
Variation of \(\langle \psi _{k’}|\psi _k\rangle\) versus \(k-k’\) with \(a=1\).
We suppose that, the wave function satisfies the Dirichlet condition i.e., it vanishes at the boundaries \(\psi _k(0)=0=\psi _k(a)\). Thus, using especially the boundary condition \(\psi _k(0)=0\), the above wavefunctions (64) becomes
$$\begin{aligned} \psi _k (y_s) = \frac{B}{\sqrt{1-\tau y_s+\tau ^2 y_s^2}}\sin \left( \frac{2k}{\tau \sqrt{3}}\left[ \arctan \left( \frac{2\tau y_s-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] \right) . \end{aligned}$$
(69)
The quantization follows from the boundary condition \(\psi _k(a)=0\) and leads to the equation
$$\begin{aligned} \frac{2k_n}{\tau \sqrt{3}}\left[ \arctan \left( \frac{2\tau a-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right]= & {} n\pi \quad \,\,\text{ with }\quad n\in {\mathbb {N}}^*, \end{aligned}$$
(70)
$$\begin{aligned} k_n= & {} \frac{\pi \tau \sqrt{3}n}{2\left[ \arctan \left( \frac{2\tau a-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] }. \end{aligned}$$
(71)
Then, the energy spectrum of the particle is written as
$$\begin{aligned} E_n’= & {} \frac{3\pi ^2 \tau ^2\hbar ^2n^2}{8m_0 \left[ \arctan \left( \frac{2\tau a-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] ^{2} }. \end{aligned}$$
(72)
At the limit \(\tau \rightarrow 0\), we have
$$\begin{aligned} \lim _{ \tau \rightarrow 0} E_n’= E_n=\frac{\pi ^2\hbar ^2n^2}{2m_0a^2}. \end{aligned}$$
(73)
Thus, the energy levels can be rewritten as
$$\begin{aligned} E_n=\frac{3}{4} \left[ \frac{\tau L}{\arctan \left( \frac{2\tau L-1}{\sqrt{3}}\right) +\frac{\pi }{6} }\right] ^2 E_n<E_n. \end{aligned}$$
(74)
The effects of the parameter \(\tau\) in \(y_s\) direction induce deformations of quantum levels, which consequently lead to a decrease in the amplitude of the energy levels. The corresponding wave functions to the energies (72) are given by
$$\begin{aligned} \psi _n (x) = \frac{B}{\sqrt{1-\tau y_s+\tau ^2 y_s^2}}\sin \left( \frac{ n\pi }{\left[ \arctan \left( \frac{2\tau a-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] ^{2}}\left[ \arctan \left( \frac{2\tau y_s-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] \right) . \end{aligned}$$
(75)
The total eigenvalues of the system are given by
$$\begin{aligned} E_n^t= & {} n^2\frac{\pi ^2\hbar ^2}{2m_0a^2}+ \frac{3\pi ^2 \tau ^2\hbar ^2n^2}{8m_0 \left[ \arctan \left( \frac{2\tau a-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] ^{2} },\nonumber \\= & {} \left( 1+\frac{3\tau ^2 a}{\left[ \arctan \left( \frac{2\tau a-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] ^{2}}\right) E_n, \end{aligned}$$
(76)
and
$$\begin{aligned} \lim _{ \tau \rightarrow 0} E_n^t =2E_n, \end{aligned}$$
(77)
The wave function in \(x_s,y_s\)-directions are given by
$$\begin{aligned} \psi (x_s,y_s)= & {} \frac{B\sqrt{\frac{2}{a}}}{\sqrt{1-\tau y_s+\tau ^2 y_s^2}} \sin \left( \frac{n\pi }{a}x_s\right) \nonumber \\&\times \sin \left( \frac{ n\pi }{\left[ \arctan \left( \frac{2\tau a-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] ^{2}}\left[ \arctan \left( \frac{2\tau y_s-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] \right) . \end{aligned}$$
(78)
At the limit \(\tau \rightarrow 0\), we have
$$\begin{aligned} \lim _{ \tau \rightarrow 0} \psi (x_s,y_s)= \frac{2}{a} \sin \left( \frac{n\pi }{a}x_s\right) \sin \left( \frac{n\pi }{a}y_s\right) . \end{aligned}$$
(79)
The corresponding probability density is given by
$$\begin{aligned} \rho (x_s,y_s)= & {} \frac{2B^2}{a(1-\tau y_s+\tau ^2 y_s^2)} \sin ^2\left( \frac{n\pi }{a}x_s\right) \nonumber \\&\times \sin^2 \left( \frac{ n\pi }{\left[ \arctan \left( \frac{2\tau a-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] ^{2}}\left[ \arctan \left( \frac{2\tau y_s-1}{\sqrt{3}}\right) +\frac{\pi }{6}\right] \right) . \end{aligned}$$
(80)
Figure 8 illustrates the energy levels of the particle as functions of the quantum number n and the quantum gravitational parameter \(\tau\). As one increases the quantum number n from the fundamental level, the increase in \(\tau\) gradually curves the energy levels (Figure (a)). For fixed values of \(\tau\), Figure (b) illustrates energy levels versus the quantum number n. Conversely to the graph obtained in68,73,74,75, one can see that, when \(\tau\) increases, the amplitudes of energy levels \(E_n^t/E_1\) decrease. In fact, by increasing the quantum gravitational effects, it leads to the enhancement of binding quantum levels allowing particles to jump from one state to another with low energies13.
Figure 9 illustrates a comparison between eigenfunctions \(\psi _n(x_s)\) and \(\psi _n(y_s)\) for fixed values of n and \(\tau\). The wave function in \(x_s\)-direction is taken as a witness with respect to that of the \(y_s\)-direction where the effects of quantum gravity are strongly applied. For \(n\in \{1;5;15;20\}\), \(\psi (y_s)\) compresses and contracts inward as one increases \(\tau\). This fact comes to confirm the fundamental property of gravity which is length contraction.
Unlike the figure reported in citations73,74,,74, Fig. 10 depicts probability density plots for the three lower states \(n = 1; n = 5; n = 15; n = 30\) for a fixed value of \(\tau\) (\(\tau = 0.1)\), it can be seen that the probability of finding a particle is practically the same everywhere in the square well and this probability strongly increases with the quantum number. This indicates that the deformations allow particles to jump from one state to another with low energies and with high probability densities.
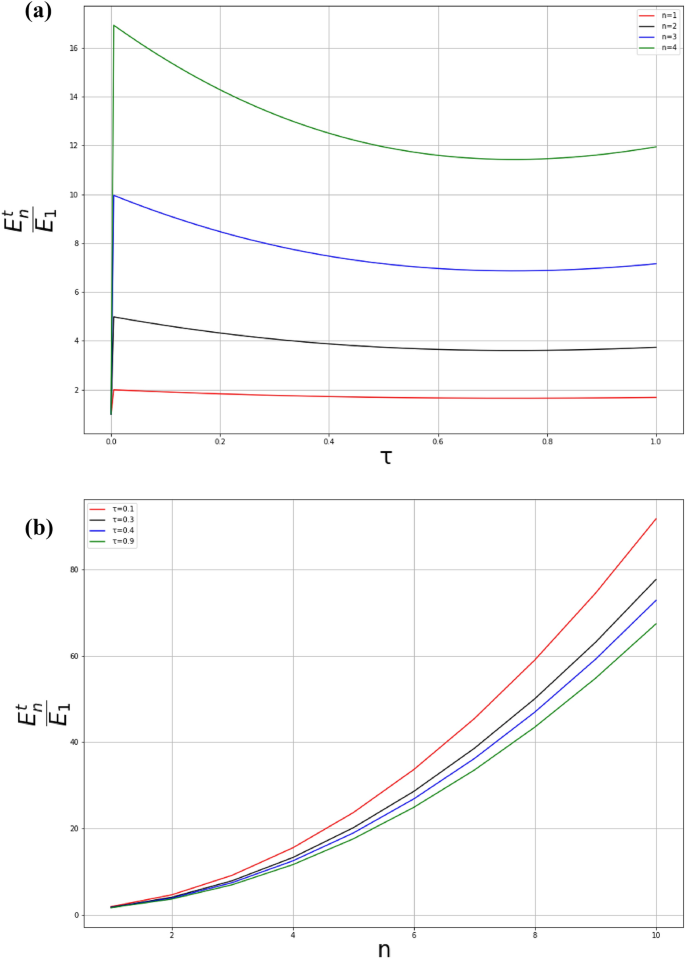
The energy \(E_n/E_1\) of the particle in 2D box of length \(a = 1\) with mass \(m_0 = 1\) and \(\hbar = 1\).
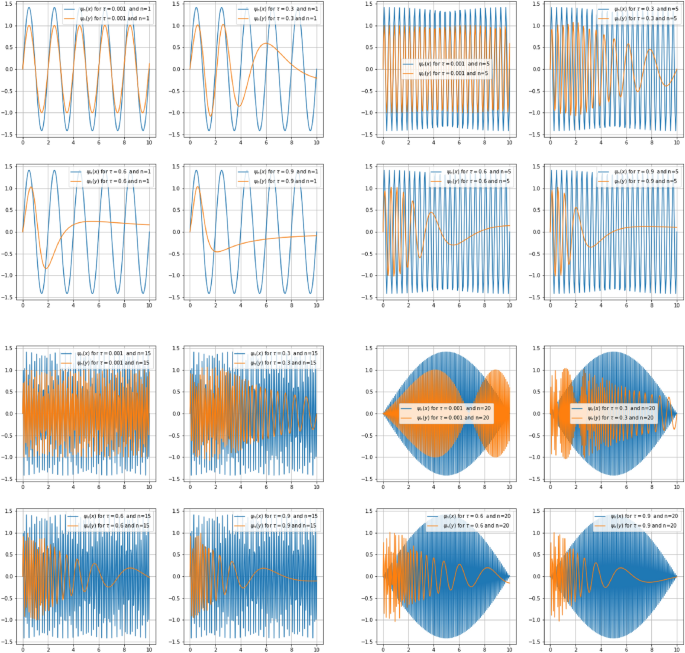
Comparison graph of \(\psi _n(x_s)\) and \(\psi _n(y_s)\) for a particle confined in an infinite square well of length \(a = 1\) deformed by the gravity parameter \(\tau\) in ys direction.
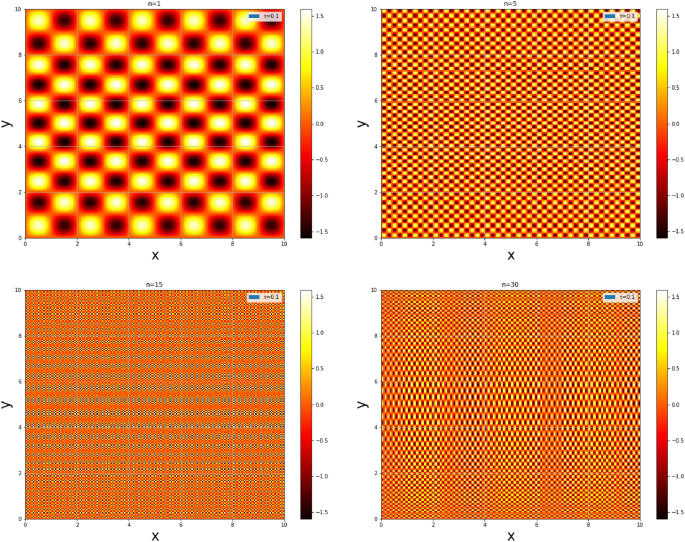
The probability density of a two-dimensional infinite square well for \(\tau = 0.1\).














 Bitcoin
Bitcoin  Ethereum
Ethereum  XRP
XRP  Tether
Tether  Solana
Solana  USDC
USDC  Dogecoin
Dogecoin  Lido Staked Ether
Lido Staked Ether  Cardano
Cardano  TRON
TRON  Wrapped stETH
Wrapped stETH  Chainlink
Chainlink  Hyperliquid
Hyperliquid  Wrapped Bitcoin
Wrapped Bitcoin  Sui
Sui  Ethena USDe
Ethena USDe  Stellar
Stellar  Avalanche
Avalanche  Wrapped eETH
Wrapped eETH  Figure Heloc
Figure Heloc  Bitcoin Cash
Bitcoin Cash  WETH
WETH  Hedera
Hedera  Litecoin
Litecoin  LEO Token
LEO Token  Cronos
Cronos  Shiba Inu
Shiba Inu  Toncoin
Toncoin  USDS
USDS  Polkadot
Polkadot  Coinbase Wrapped BTC
Coinbase Wrapped BTC  Binance Bridged USDT (BNB Smart Chain)
Binance Bridged USDT (BNB Smart Chain)  WhiteBIT Coin
WhiteBIT Coin  Uniswap
Uniswap  Ethena Staked USDe
Ethena Staked USDe  World Liberty Financial
World Liberty Financial  Mantle
Mantle  Ethena
Ethena  Monero
Monero  Pepe
Pepe  Aave
Aave  Bitget Token
Bitget Token  Dai
Dai  OKB
OKB  MemeCore
MemeCore  NEAR Protocol
NEAR Protocol  Jito Staked SOL
Jito Staked SOL  Ondo
Ondo