We linearly perturb the relevant physical fluid parameters appearing in Eqs. (14), (15.1), (15.2), (16), (17), (18) and (19), using a cylindrical wave analysis24 in an autonormalized Fourier transformed wavespace given as
$$F\left( {R,\,\tau } \right) = F_{0} + \,F_{1} \left( {R,\,\tau } \right)\, = F_{0} + F_{10} \exp \left( { – i\Omega \tau } \right)H_{0}^{\left( 1 \right)} \left( {k^{*} R} \right)\,\,,$$
(20)
where \(H_{0}^{\left( 1 \right)}\) is the Hankel function of the first kind, of order 0.
For \(R \to 0\), \(H_{0}^{\left( 1 \right)}\) has logarithmic singularity:
$$H_{0}^{\left( 1 \right)} = \left( {2i\pi^{ – 1} } \right)\log \left( {k^{*} R} \right)$$
(21)
At large distances, we have
$$H_{0}^{\left( 1 \right)} = \left( {2\pi^{ – 1} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {k^{*} R} \right)^{{ – {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \exp \left[ {i\left( {k^{*} R – \pi 4^{ – 1} } \right)} \right]$$
(22)
Thus, Eq. (20) gets modified as
$$F\left( {R,\,\tau } \right) = F_{0} + \,F_{1} \left( {R,\,\tau } \right)\, = F_{0} + F_{10} \left( {2\pi^{ – 1} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {k^{*} R} \right)^{{ – {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \exp \left[ {i\left( {k^{*} R – \Omega \tau – \pi 4^{ – 1} } \right)} \right]\,,$$
(23)
$$F = \left[ {N_{s} \,\,\,\,\,\,\,\,M_{s} \,\,\,\,\,\,\,\,\Phi_{E} \,\,\,\,\,\,\,\,\,\,\Psi } \right]^{T} ,$$
(24)
$$F_{0} = \left[ {1\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,0\,} \right]^{T} \,,$$
(25)
$$F_{1} = \left[ {N_{s1} \,\,\,\,M_{s1} \,\,\,\,\,\,\Phi_{E1} \,\,\,\,\,\,\,\Psi_{1} \,} \right]^{T} .$$
(26)
Here, we assume an axisymmetric cylinder such that all quantities are homogeneously distributed along z-direction, and thereby just show radial variations. In Eq. (23), F1 denotes the radial perturbations, which evolve as per the Hankel function of first kind of order 0. F0 denotes the equilibrium values corresponding to which perturbations F1 take place. In the new Fourier transformed wavespace, the spatial and temporal operators get transformed as \({\partial \mathord{\left/ {\vphantom {\partial {\partial R \to \left( {\,ik^{*} – \,\,{1 \mathord{\left/ {\vphantom {1 R}} \right. \kern-0pt} R}} \right)}}} \right. \kern-0pt} {\partial R \to \left( {\,ik^{*} – \,\,{1 \mathord{\left/ {\vphantom {1 R}} \right. \kern-0pt} R}} \right)}}\) and \({\partial \mathord{\left/ {\vphantom {\partial {\partial \tau \to \left( { – i\,\,\Omega } \right)}}} \right. \kern-0pt} {\partial \tau \to \left( { – i\,\,\Omega } \right)}}\), respectively. Here, \(\Omega\) \(\left( {{{ = \omega } \mathord{\left/ {\vphantom {{ = \omega } {\omega_{pi} }}} \right. \kern-0pt} {\omega_{pi} }}} \right)\) denotes the normalized fluctuation frequency and \(k^{*} \left( {\sim {k \mathord{\left/ {\vphantom {k {L_{0}^{ – 1} }}} \right. \kern-0pt} {L_{0}^{ – 1} }}} \right)\) designates the normalized wavenumber. The linearly perturbed relevant physical parameters from Eqs. (14), (15.1), (15.2), (16), (17), (18) and (19) in the new wave space can respectively be cast as
$$N_{e1} = – i\Omega^{ – 1} \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}M_{e1} ,$$
(27)
$$M_{e1} = E^{ – 1} \left( {m_{i} m_{e}^{ – 1} } \right)\left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}\Phi_{E1} – iE^{ – 1} \Omega^{ – 1} \sigma \left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} M_{i1} ,$$
(28)
$$N_{i1} = – i\Omega^{ – 1} \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}M_{i1} ,$$
(29)
$$M_{i1} = – H^{ – 1} \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}\Phi_{E1} \left[ {1 + i\Omega^{ – 1} E^{ – 1} \sigma \left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} } \right],$$
(30)
$$\Phi_{E1} = – i\Omega^{ – 1} \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left( {M_{e1} – M_{i1} } \right),$$
(31)
$$\Psi_{1} = – i\Omega^{ – 1} \sigma \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left\{ {\left( {m_{e} m_{i}^{ – 1} } \right)M_{e1} + M_{i1} } \right\}.$$
(32)
In the above set of Eqs. (27), (28), (29), (30), (31) and (32), the various substituted terms are given as
$$E = – i\Omega + i\Omega^{ – 1} \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}\left. {\left[ {{ – }\Omega_{ge}^{*} M_{e\varphi } + 4^{ – 1} H_{p}^{2} B_{p} + 2M_{\varphi } \omega_{z}^{*} + } \right.\left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}\left[ {\alpha – \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \sigma m_{e} m_{i}^{ – 1} } \right]} \right]$$
(33)
$$B_{p} = – ik^{{*^{3} }} + k^{{*^{2} }} \left( {2R} \right)^{ – 1} + ik^{*} \left( {4R^{2} } \right)^{ – 1} – 5\left( {8R^{3} } \right)^{ – 1}$$
(34)
$$\alpha = \left( 3 \right)^{ – 1} M_{Fe}^{2} ,\,{\text{for CDcase}},{\text{ where}}\,M_{Fe} = {{v_{Fe} } \mathord{\left/ {\vphantom {{v_{Fe} } {c_{s} }}} \right. \kern-0pt} {c_{s} }}\,{\text{and}}\,v_{Fe} = \left( {3\pi^{2} n_{e} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} \hbar \,m_{e}^{ – 1}$$
(35)
$$\alpha = m_{i} m_{e}^{ – 1} T^{*} ,\,{\text{for CND}}\,{\text{case, }}$$
(36)
$$\begin{aligned} H = & – i\Omega + i\Omega^{ – 1} \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}\left. {\left[ {\Omega_{gi}^{*} M_{i\varphi } + 2M_{\varphi } \omega_{z}^{*} + } \right.\left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}\left[ {T^{*} – \sigma \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} } \right]} \right] \\ & – \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\eta^{*} + \Omega^{ – 2} \left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{2} \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \sigma^{2} m_{e} m_{i}^{ – 1} E^{ – 1} \\ \end{aligned}$$
(37)
After a standard procedure of elimination and substitution among Eqs. (27), (28), (29), (30), (31), (32), (33), (34), (35), (36) and (37), we obtain a generalized linear sextic dispersion relation cast as
$$\Omega^{6} + A_{5} \Omega^{5} + A_{4} \Omega^{4} + A_{3} \Omega^{3} + A_{2} \Omega^{2} + A_{1} \Omega + A_{0} = 0$$
(38)
The different coefficients in an expanded form are given as
$$A_{5} = – i\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\,\eta^{*}$$
(39)
$$A_{4} = \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}\,\,\left[ { – 2\Omega_{ge}^{*} M_{e\varphi }^{*} + \left( {2\alpha + T^{*} } \right)} \right.\left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\} – 2^{ – 1} H_{p}^{2} B_{p} + 6M_{\varphi } \omega_{z}^{*} + \Omega_{gi}^{*} M_{i\varphi }^{*}$$
$$\left. { + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left\{ {m_{i} m_{e}^{ – 1} + 1 – \sigma \left( {2m_{e} m_{i}^{ – 1} + 1} \right)} \right\}} \right]$$
(40)
$$A_{3} = – i\left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}\eta^{*} \left[ {\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\,\,\,\left[ {2\Omega_{ge}^{*} M_{e\varphi }^{*} + 2^{ – 1} H_{p}^{2} B_{p} – 4M_{\varphi } \omega_{z}^{*} – 2\alpha \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}} \right]} \right.$$
$$\left. { + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}\left( {2\sigma m_{e} m_{i}^{ – 1} – m_{i} m_{e}^{ – 1} } \right)} \right],$$
(41)
$$A_{2} = – \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}^{2} \left[ {\,\left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}\,\left[ { – 2\alpha \,\left( {\Omega_{ge}^{*} M_{e\varphi }^{*} – \Omega_{gi}^{*} M_{i\varphi }^{*} } \right) + 2^{ – 1} H_{p}^{2} B_{p} \alpha + 4M_{\varphi } \omega_{z}^{*} \left( {\alpha + T^{*} } \right)} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \right.$$
$$- 2\left( {\Omega_{ge}^{*} M_{e\varphi }^{*} T^{*} – 2M_{\varphi } \omega_{z}^{*} \alpha } \right) – 2^{ – 1} T^{*} H_{p}^{2} B_{p} + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left[ {2\Omega_{ge}^{*} M_{e\varphi } \sigma \left( {1 + m_{e} m_{i}^{ – 1} } \right)} \right.$$
$$- 2^{ – 1} H_{p}^{2} B_{p} \sigma \left( { – 1 + m_{e} m_{i}^{ – 1} } \right) – 2\sigma \left\{ {\left( {\Omega_{gi}^{*} M_{i\varphi } + 4M_{\varphi } \omega_{z}^{*} } \right)m_{e} m_{i}^{ – 1} + 2M_{\varphi } \omega_{z}^{*} } \right\} + 2\left\{ {\Omega_{ge}^{*} M_{e\varphi } + 2M_{\varphi } \omega_{z}^{*} } \right.$$
$$\left. {\left. {\left. { – 4^{ – 1} H_{p}^{2} B_{p} } \right\} + m_{i} m_{e}^{ – 1} \left( {\Omega_{gi}^{*} M_{i\varphi } + 4M_{\varphi } \omega_{z}^{*} – \Omega_{ge}^{*} M_{e\varphi } + 4^{ – 1} H_{p}^{2} B_{p} } \right)} \right]\,\,} \right]\, + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}^{2} \left[ {\alpha^{2} } \right.$$
$$+ 2\alpha T^{*} + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left[ { – 2\sigma \left\{ {\left( {T^{*} + 1} \right)m_{e} m_{i}^{ – 1} + 1} \right\}} \right. + 2\alpha + m_{i} m_{e}^{ – 1} \left. {\left( {T^{*} + \alpha } \right)} \right] + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2}$$
$$\left. {\left[ { – \sigma \left( {1 + m_{i} m_{e}^{ – 1} } \right)} \right. – 2\sigma m_{e} m_{i}^{ – 1} + \sigma^{2} m_{e} m_{i}^{ – 1} \left. {\left( {1 + m_{e} m_{i}^{ – 1} } \right) + 2\sigma } \right]\,\,} \right] – 2^{ – 1} H_{p}^{2} B_{p} \left( {\Omega_{ge}^{*} M_{e\varphi }^{*} + \Omega_{gi}^{*} M_{i\varphi }^{*} } \right)$$
$$\left. { – 8M_{\varphi } \omega_{z}^{*} \Omega_{ge}^{*} M_{e\varphi } + \left( {\Omega_{ge}^{*} M_{e\varphi }^{*} } \right)^{2} + \left( {4^{ – 1} H_{p}^{2} B_{p} } \right)^{2} + 2\Omega_{gi}^{*} M_{i\varphi } \left( { – \Omega_{ge}^{*} M_{e\varphi }^{*} + 2M_{\varphi } \omega_{z}^{*} } \right) + 12\left( {M_{\varphi } \omega_{z}^{*} } \right)^{2} } \right],$$
(42)
$$A_{1} = – i\left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}^{2} \eta^{*} \,\left[ {\,\left[ {\left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}\left[ {\left( {\Omega_{ge}^{*} M_{e\varphi } – 4^{ – 1} H_{p}^{2} B_{p} – 2M_{\varphi } \omega_{z}^{*} } \right)\left[ {2\sigma m_{e} m_{i}^{ – 1} – m_{i} m_{e}^{ – 1} } \right.} \right.} \right.} \right.$$
$$\left. {\left. { – 2\alpha \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}} \right]\,\,} \right]\, + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\,\,\left[ {\Omega_{ge}^{*} M_{e\varphi } \left( {\Omega_{ge}^{*} M_{e\varphi } – 2^{ – 1} H_{p}^{2} B_{p} – 4M_{\varphi } \omega_{z}^{*} } \right)} \right.$$
$$\left. {\left. { + 4^{ – 1} H_{p}^{2} B_{p} \left( {4^{ – 1} H_{p}^{2} B_{p} + 4M_{\varphi } \omega_{z}^{*} } \right) + 4\left( {M_{\varphi } \omega_{z}^{*} } \right)^{2} } \right]\,\,} \right] + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}^{2} \left[ { – 2\alpha \sigma \,m_{e} m_{i}^{ – 1} } \right. + \alpha \,m_{i} m_{e}^{ – 1}$$
$$\left. {\left. { + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left( {\sigma \,m_{e} m_{i}^{ – 1} – m_{i} m_{e}^{ – 1} } \right) + 2\alpha^{2} \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}} \right]\,\,} \right]$$
(43)
$$A_{0} = \left[ { – P + \left[ {\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} m_{i} m_{e}^{ – 1} Q} \right] + \left[ {2\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{2} \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \sigma S} \right]} \right.$$
$$\left. { – \left[ {\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{3} \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \sigma^{2} } \right] + \left[ {\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} I} \right]} \right]$$
(44)
The different terms substituted in A0 are given in an expanded form as
$$P = – \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}^{3} \left[ {\left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}\left[ {\,\left[ {2\alpha \Omega_{gi}^{*} M_{i\varphi } \left( {\Omega_{ge}^{*} M_{e\varphi } – 2M_{\varphi } \omega_{z}^{*} } \right)} \right.} \right.} \right. – 4^{ – 1} H_{p}^{2} B_{p} \left\{ {2\alpha \Omega_{gi}^{*} M_{i\varphi } } \right. + 4\left. {\left( {T^{*} + \alpha } \right)M_{\varphi } \omega_{z}^{*} } \right\}$$
$$- \Omega_{ge}^{*} M_{e\varphi } T^{*} \left( {\Omega_{ge}^{*} M_{e\varphi } – 4M_{\varphi } \omega_{z}^{*} } \right) – 4^{ – 1} H_{p}^{2} B_{p} T^{*} \left\{ { – 2\Omega_{ge}^{*} M_{e\varphi } } \right. + \left. {4^{ – 1} H_{p}^{2} B_{p} } \right\} – 4M_{\varphi } \omega_{z}^{*} \left\{ {T^{*} } \right.M_{\varphi } \omega_{z}^{*}$$
$$\left. {\left. { + \left( {2M_{\varphi } \omega_{z}^{*} – \Omega_{ge}^{*} M_{e\varphi } } \right)\alpha } \right\}} \right]\, + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left[ { – 2\Omega_{gi}^{*} M_{i\varphi } \sigma \,m_{e} m_{i}^{ – 1} \left( {\Omega_{ge}^{*} M_{e\varphi } – 4^{ – 1} H_{p}^{2} B_{p} – 4M_{\varphi } \omega_{z}^{*} } \right)} \right.$$
$$- 4\sigma m_{e} m_{i}^{ – 1} M_{\varphi } \omega_{z}^{*} \left( {\Omega_{ge}^{*} M_{e\varphi } – 4^{ – 1} H_{p}^{2} B_{p} – 2M_{\varphi } \omega_{z}^{*} } \right) + \sigma 4^{ – 1} H_{p}^{2} B_{p} \left( {4^{ – 1} H_{p}^{2} B_{p} + 4M_{\varphi } \omega_{z}^{*} } \right)$$
$$\left. {\left. { – 2\Omega_{ge}^{*} M_{e\varphi } \sigma \left\{ {2M_{\varphi } \omega_{z}^{*} \left( {1 – M_{\varphi } \omega_{z}^{*} } \right) + 4^{ – 1} H_{p}^{2} B_{p} – 2^{ – 1} \Omega_{ge}^{*} M_{e\varphi } } \right\}} \right]\,} \right] + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}^{2} \left[ {\left[ { – \alpha \left( {\alpha \Omega_{gi}^{*} M_{i\varphi } } \right.} \right.} \right.$$
$$\left. {\left. { – 2\Omega_{ge}^{*} M_{e\varphi } T^{*} + \,\,2\alpha M_{\varphi } \omega_{z}^{*} \,} \right) – 2\alpha T^{*} \left( {2M_{\varphi } \omega_{z}^{*} + 4^{ – 1} H_{p}^{2} B_{p} } \right)} \right] + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left[ {\sigma m_{e} m_{i}^{ – 1} } \right.\left\{ {\Omega_{gi}^{*} M_{i\varphi } \alpha \,} \right.$$
$$\left. {\left. { + T^{*} \left( {2M_{\varphi } \omega_{z}^{*} – \Omega_{ge}^{*} M_{e\varphi } } \right.} \right) + m_{i} m_{e}^{ – 1} \alpha 4^{ – 1} H_{p}^{2} B_{p} } \right\} + \sigma m_{e} m_{i}^{ – 1} \left\{ {2^{ – 1} H_{p}^{2} B_{p} T + 4\alpha M_{\varphi } \omega_{z}^{*} + 2} \right.m_{i} m_{e}^{ – 1} \left( {2\alpha } \right.M_{\varphi } \omega_{z}^{*}$$
$$\left. {\left. {\left. { – \Omega_{ge}^{*} M_{e\varphi } } \right)} \right\}} \right] + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \left[ { – \sigma^{2} \left( {m_{e} m_{i}^{ – 1} } \right)^{2} } \right.\left( {\Omega_{{{\text{gi}}}}^{*} M_{i\varphi } – 2m_{i} m_{e}^{ – 1} \Omega_{{{\text{ge}}}}^{*} M_{e\varphi } + 2M_{\varphi } \omega_{z}^{*} } \right) + \sigma^{2} m_{e} m_{i}^{ – 1}$$
$$\left. {\left. {\left( {2^{ – 1} M_{\varphi } \omega_{z}^{*} + \Omega_{ge}^{*} M_{e\varphi } \, + 4^{ – 1} H_{p}^{2} B_{p} } \right)} \right]\,} \right]\,\, + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}^{3} \left[ { – \alpha^{2} } \right.T^{*} + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left( {2\alpha \sigma m_{e} m_{i}^{ – 1} T^{*} + \alpha^{2} \sigma^{2} } \right)$$
$$\left. { + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \left\{ { – T^{*} \sigma^{2} \left( {m_{e} m_{i}^{ – 1} } \right)^{2} – \alpha \sigma^{2} m_{e} m_{i}^{ – 1} } \right\}} \right]\, + \Omega_{{{\text{gi}}}}^{*} M_{i\varphi } \Omega_{{{\text{ge}}}}^{*} M_{e\varphi } \left( { – \Omega_{{{\text{ge}}}}^{*} M_{e\varphi } + 4M_{\varphi } \omega_{z}^{*} } \right)$$
$$+ 2^{ – 1} H_{p}^{2} B_{p} \Omega_{{{\text{gi}}}}^{*} M_{i\varphi } \left( {\Omega_{{{\text{ge}}}}^{*} M_{e\varphi } – 2M_{\varphi } \omega_{z}^{*} } \right) – \Omega_{{{\text{gi}}}}^{*} M_{i\varphi } \left( {4^{ – 1} H_{p}^{2} B_{p} } \right)^{2} – 4\left( {M_{\varphi } \omega_{z}^{*} } \right)^{2} \left( {\Omega_{{{\text{gi}}}}^{*} M_{i\varphi } – 2\Omega_{{{\text{ge}}}}^{*} M_{e\varphi } + 2M_{\varphi } \omega_{z}^{*} } \right)$$
$$\left. { + 2\Omega_{{{\text{ge}}}}^{*} M_{e\varphi } M_{\varphi } \omega_{z}^{*} \left( { – \Omega_{{{\text{ge}}}}^{*} M_{e\varphi } + 2^{ – 1} H_{p}^{2} B_{p} } \right) – M_{\varphi } \omega_{z}^{*} 2^{ – 1} H_{p}^{2} B_{p} \left( {4^{ – 1} H_{p}^{2} B_{p} + 4M_{\varphi } \omega_{z}^{*} } \right)} \right]$$
(45)
$$\left[ {\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} m_{i} m_{e}^{ – 1} Q} \right]$$
$$= – \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}^{3} \left[ {\left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}} \right.\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left[ {m_{i} m_{e}^{ – 1} } \right.\Omega_{{{\text{ge}}}}^{*} M_{e\varphi } \left( {\Omega_{{{\text{gi}}}}^{*} M_{i\varphi } + 2M_{\varphi } \omega_{z}^{*} } \right)$$
$$\left. { – 4M_{\varphi } \omega_{z}^{*} m_{i} m_{e}^{ – 1} \left( {\Omega_{{{\text{gi}}}}^{*} M_{i\varphi } + M_{\varphi } \omega_{z}^{*} } \right) – m_{i} m_{e}^{ – 1} 2^{ – 1} H_{p}^{2} B_{p} M_{\varphi } \omega_{z}^{*} } \right] + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}^{2} \left[ {\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} } \right.$$
$$\left. {\left[ {m_{i} m_{e}^{ – 1} \left\{ {\Omega_{{{\text{ge}}}}^{*} M_{e\varphi } – \alpha \left( {\Omega_{{{\text{gi}}}}^{*} M_{i\varphi } + 2M_{\varphi } \omega_{z}^{*} } \right)} \right\} – } \right.m_{i} m_{e}^{ – 1} T^{*} \left( {4^{ – 1} H_{p}^{2} B_{p} + 2M_{\varphi } \omega_{z}^{*} } \right)} \right] + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2}$$
$$\left. {\left[ { – \sigma m_{i} m_{e}^{ – 1} \left( {\Omega_{{{\text{ge}}}}^{*} M_{e\varphi } – 4^{ – 1} H_{p}^{2} B_{p} – 2M_{\varphi } \omega_{z}^{*} } \right) + \sigma \left( {\Omega_{{{\text{gi}}}}^{*} M_{i\varphi } + 2M_{\varphi } \omega_{z}^{*} } \right)} \right]\,} \right] + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}^{3} \left[ { – \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} } \right.$$
$$\left. {\left. {\alpha m_{i} m_{e}^{ – 1} T^{*} + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \sigma m_{i} m_{e}^{ – 1} \left( {\alpha + m_{e} m_{i}^{ – 1} } \right)} \right]} \right]$$
(46)
$$\left[ {2\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{2} \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \sigma S} \right]$$
$$= – 2\sigma \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}^{3} \left[ { – \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}^{2} } \right.\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \left( {\Omega_{{{\text{ge}}}}^{*} M_{e\varphi } – 4^{ – 1} H_{p}^{2} B_{p} – 2M_{\varphi } \omega_{z}^{*} } \right)$$
$$\left. { + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}^{3} \,\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \left[ {\alpha – \sigma \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} m_{e} m_{i}^{ – 1} } \right]} \right],$$
(47)
$$\left[ {\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} I} \right]$$
$$= – \left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}^{3} \left[ {\left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}} \right.\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left[ {\Omega_{{{\text{ge}}}}^{*} M_{e\varphi } \left( { – \Omega_{{{\text{ge}}}}^{*} M_{e\varphi } + 2^{ – 1} H_{p}^{2} B_{p} + 4M_{\varphi } \omega_{z}^{*} } \right)} \right.$$
$$\left. { – 4^{ – 1} H_{p}^{2} B_{p} \left( {4^{ – 1} H_{p}^{2} B_{p} + 4M_{\varphi } \omega_{z}^{*} } \right) – 4\left( {M_{\varphi } \omega_{z}^{*} } \right)^{2} } \right] + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}^{2} \left[ { – \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left( { – \Omega_{{{\text{ge}}}}^{*} M_{e\varphi } } \right.} \right.$$
$$\left. {\left. { + 4^{ – 1} H_{p}^{2} B_{p} + 2M_{\varphi } \omega_{z}^{*} } \right) + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \left\{ { – 2\sigma \left. {m_{e} m_{i}^{ – 1} \left( {2\Omega_{{{\text{ge}}}}^{*} M_{e\varphi } – 4^{ – 1} H_{p}^{2} B_{p} – 2M_{\varphi } \omega_{z}^{*} } \right.} \right)} \right\}} \right]$$
$$\left. { + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}^{3} \left[ { – \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \alpha^{2} + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \left( {2\alpha \sigma m_{e} m_{i}^{ – 1} } \right) – \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 3} \left( {\sigma m_{e} m_{i}^{ – 1} } \right)^{2} } \right]} \right]$$
(48)
The sextic dispersion relation (Eq. (38)) is transformed into a reduced form in light of the LF approximation with the help of traditional simplification procedure34. We are primarily interested in the LF limit because we wish to investigate the cylindrical acoustic waves. In the LF limit \(\left( {\Omega^{q} = 0\,,\,\forall \,q > \,1} \right)\), the modified dispersion relation is
$$A_{1} \Omega + A_{0} = 0$$
(49)
The coefficients \(A_{1}\)–\(A_{0}\) are given in Eqs. (43) and (44), respectively. We then analyze the dispersion relation in four distinct regimes of our interest, namely in quantum (CD) non-planar (cylindrical), quantum planar, classical (CND) non-planar (cylindrical), classical (CND) planar.
Quantum (CD) non-planar regime
In the quantum non-planar regime, we have the same dispersion relation as given by Eq. (49). Likewise, the coefficients are the same as given by Eqs. (43) and (44).\(\alpha\) for the CD case is substituted from Eq. (35).
Quantum (CD) planar regime
In the quantum planar regime, we have \(R \to \infty\). The dispersion relation is the same as Eq. (49). However, the coefficients given by Eqs. (43) and (44) are modified. \(\alpha\) for the CD case is substituted from Eq. (35). The cylindrical coordinates are mapped into planar coordinates accordingly. The modified coefficients are given as
$$A_{1} = ik^{{*^{2} }} \eta^{*} \,\left[ {\,\left[ {\left( {ik^{*} } \right)\left[ {\left( {\Omega_{ge}^{*} M_{ey} – 4^{ – 1} H_{p}^{2} B_{p} – 2M_{y} \omega_{z}^{*} } \right)\left[ {2\sigma m_{e} m_{i}^{ – 1} – m_{i} m_{e}^{ – 1} } \right.} \right.} \right.} \right.\left. {\left. { + 2\alpha k^{{*^{2} }} } \right]\,} \right]$$
$$- k^{{*^{2} }} \,\,\left[ {\Omega_{ge}^{*} M_{ey} \left( {\Omega_{ge}^{*} M_{ey} – 2^{ – 1} H_{p}^{2} B_{p} – 4M_{y} \omega_{z}^{*} } \right)} \right.\left. {\left. { + 4^{ – 1} H_{p}^{2} B_{p} \left( {4^{ – 1} H_{p}^{2} B_{p} + 4M_{y} \omega_{z}^{*} } \right) + 4\left( {M_{y} \omega_{z}^{*} } \right)^{2} } \right]\,\,} \right]$$
$$- k^{{*^{2} }} \left[ { – 2\alpha \sigma \,m_{e} m_{i}^{ – 1} } \right. + \alpha \,m_{i} m_{e}^{ – 1} \left. {\left. { – k^{{*^{ – 2} }} \left( {\sigma \,m_{e} m_{i}^{ – 1} – m_{i} m_{e}^{ – 1} } \right) – 2\alpha^{2} k^{{*^{2} }} } \right]\,\,} \right]$$
(50)
$$A_{0} = \left[ { – P – \left( {m_{i} m_{e}^{ – 1} Q} \right)} \right. – \left( {2\sigma S} \right) – \left. {k^{{*^{2} }} \sigma^{2} – I} \right]$$
(51)
The different substituted terms in Eq. (51) are modified accordingly.
Classical (CND) non-planar regime
In the classical non-planar regime, the Bohm potential term is ignored. The dispersion relation is the same as Eq. (49), however, the coefficients \(A_{1}\) and \(A_{0}\) are modified. \(\alpha\) for the classical case is substituted from Eq. (36). The coefficients are modified as
$$A_{1} = – i\left\{ {ik^{*} + \,\left( {2R} \right)^{ – 1} \,} \right\}^{2} \eta^{*} \,\left[ {\,\left[ {\left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}\left[ {\left( {\Omega_{ge}^{*} M_{e\varphi } – 2M_{\varphi } \omega_{z}^{*} } \right)\left[ {2\sigma m_{e} m_{i}^{ – 1} – m_{i} m_{e}^{ – 1} } \right.} \right.} \right.} \right.\left. {\left. { – 2\alpha \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}} \right]\,\,} \right]$$
$$\, + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\,\,\left[ {\Omega_{ge}^{*} M_{e\varphi } \left( {\Omega_{ge}^{*} M_{e\varphi } – 4M_{\varphi } \omega_{z}^{*} } \right)} \right.\left. {\left. { + 4\left( {M_{\varphi } \omega_{z}^{*} } \right)^{2} } \right]\,\,} \right] + \left\{ {ik^{*} – \,\left( {2R} \right)^{ – 1} \,} \right\}^{2} \left[ { – 2\alpha \sigma \,m_{e} m_{i}^{ – 1} } \right. + \alpha \,m_{i} m_{e}^{ – 1}$$
$$\left. {\left. { + \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} \left( {\sigma \,m_{e} m_{i}^{ – 1} – m_{i} m_{e}^{ – 1} } \right) + 2\alpha^{2} \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}} \right]\,\,} \right]$$
(52)
$$A_{0} = \left[ { – P + \left[ {\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} m_{i} m_{e}^{ – 1} Q} \right] + \left[ {2\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{2} \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \sigma S} \right]} \right.$$
$$\left. { – \left[ {\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{3} \left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 2} \sigma^{2} } \right] + \left[ {\left\{ {k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}\left\{ { – k^{{*^{2} }} + \left( {4R^{2} } \right)^{ – 1} } \right\}^{ – 1} I} \right]} \right]$$
(53)
The different substituted terms appearing in Eq. (53) are modified as per the approximations stated in “Classical non-planar regime” section.
Classical (CND) planar regime
In the classical (CND) planar regime, we have \(R \to \infty\). Just like the classical non-planar regime, Bohm potential is also ignored herein. The dispersion relation is the same as given by Eq. (49). The coefficients appearing in Eq. (49) are modified as per the considered regime. The cylindrical coordinates are conveniently mapped into planar coordinates. \(\alpha\) for the classical case is substituted from Eq. (36). The modified coefficients A1 and A0 are given as
$$A_{1} = ik^{{*^{2} }} \eta^{*} \,\left[ {\,\left[ {\left( {ik^{*} } \right)\left[ {\left( {\Omega_{ge}^{*} M_{ey} – 2M_{y} \omega_{z}^{*} } \right)\left[ {2\sigma m_{e} m_{i}^{ – 1} – m_{i} m_{e}^{ – 1} } \right.} \right.} \right.} \right.\left. {\left. { + 2\alpha k^{{*^{2} }} } \right]\,} \right] – k^{{*^{2} }} \,\,\left[ {\Omega_{ge}^{*} M_{ey} \left( {\Omega_{ge}^{*} M_{ey} – 4M_{y} \omega_{z}^{*} } \right)} \right.\left. {\left. { + 4\left( {M_{y} \omega_{z}^{*} } \right)^{2} } \right]\,\,} \right]$$
$$- k^{{*^{2} }} \left[ { – 2\alpha \sigma \,m_{e} m_{i}^{ – 1} } \right. + \alpha \,m_{i} m_{e}^{ – 1} \left. {\left. { – k^{{*^{ – 2} }} \left( {\sigma \,m_{e} m_{i}^{ – 1} – m_{i} m_{e}^{ – 1} } \right) – 2\alpha^{2} k^{{*^{2} }} } \right]\,\,} \right],$$
(54)
$$A_{0} = \left[ { – P – \left( {m_{i} m_{e}^{ – 1} Q} \right)} \right. – \left( {2\sigma S} \right) – \left. {k^{{*^{2} }} \sigma^{2} – I} \right]$$
(55)
The different terms appearing in Eq. (55) are modified as per our approximations (as in “Classical planar regime” section).
The above discussion in the subsections are summarily pointed out as
-
In the quantum non-planar regime, the dispersion relation has the contribution due to the geometric curvature effect, Lorentz force, Coriolis rotational force, kinematic viscosity, quantum parameter, Bohm potential, quantum pressure, temperature, and Jeans-to-plasma oscillation frequency ratio squared. The growth patterns for different parameters are depicted in Figs. 1, 2, 3, 4 and 5.
-
In the quantum planar regime, the reduced dispersion relation has the dependencies of all the above terms except the geometric curvature. The growth/damping trends of the same for different relevant parameters are given in Figs. 6, 7, 8, 9 and 10.
-
For the classical non-planar regime, the dispersion relation has the dependencies of all the terms as the quantum non-planar regime, except the Bohm potential term. The quantum pressure also gets replaced with the classical pressure. The growth/damp trends for the same are given in Figs. 11, 12, 13, 14 and 15.
-
Lastly, for the classical planar regime, the dispersion relation highlights the contribution of all the terms as the classical non-planar regime, except the geometric curvature terms. The growth/damp trends for the relevant parameters in this regime are graphically seen in Figs. 16, 17, 18, 19 and 20.
Profile of the normalized growth rate \(\left( {\Omega_{i} } \right)\) with variation in the normalized wavenumber \(\left( {k^{*} } \right)\). The different lines link to different values of the equilibrium number density \(\left( {n_{0} } \right)\) in non-planar (cylindrical) geometry in the quantum regime (\(\hbar \ne 0\)).
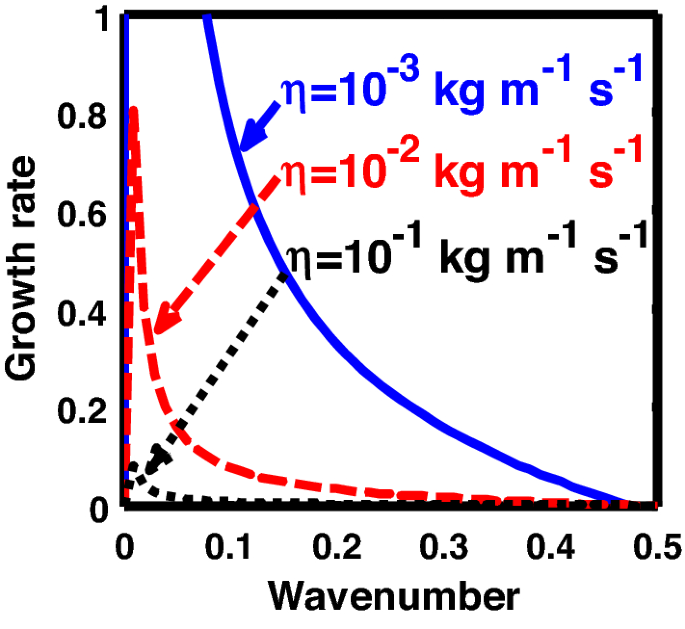
Same as Fig. 1, but for different values of the normalized kinematic viscosity \(\left( {\eta^{*} } \right)\).
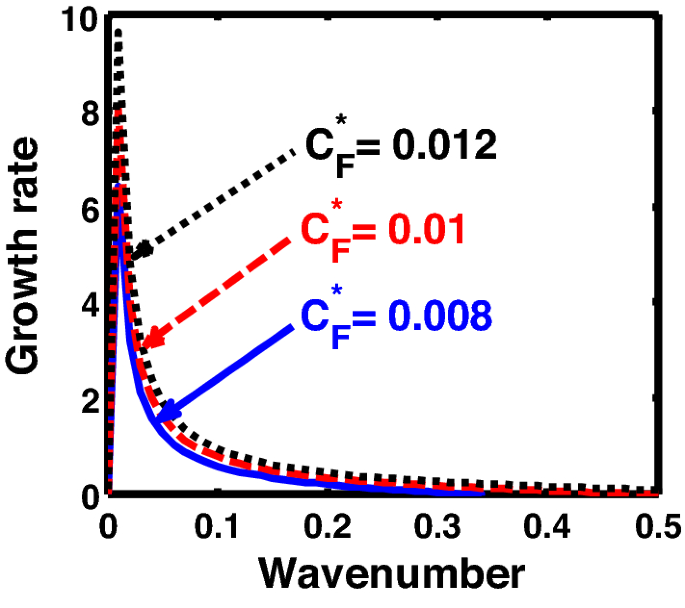
Same as Fig. 1, but for different values of the normalized Coriolis rotational force \(\left( {C_{F}^{*} } \right)\).
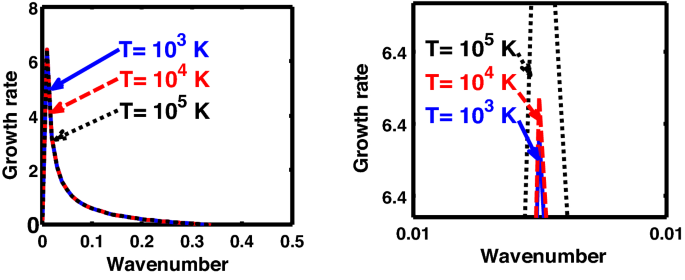
Same as Fig. 1, but for different values of the normalized thermal temperature \(\left( {T^{*} } \right)\). The second subplot is the magnified version depicting the peaks (kinks) clearly.
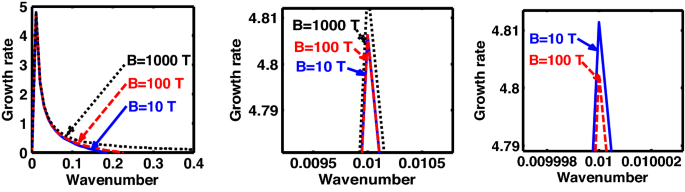
Same as Fig. 1, but for different values of magnetic field \(\left( B \right)\). The two subsequent subplots depict the magnified versions clearly highlighting the peaks (kinks).
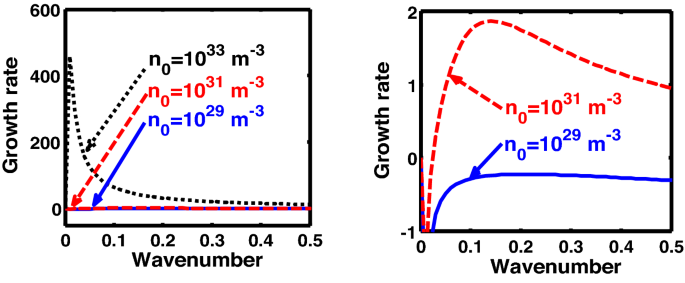
Profile of the normalized growth rate \(\left( {\Omega_{i} } \right)\) with variation in the normalized wavenumber \(\left( {k^{*} } \right)\). The different lines link to different values of the equilibrium number density \(\left( {n_{0} } \right)\) in planar (non-cylindrical) geometry in the quantum regime. The second subplot is the enlarged version highlighting the trends for \(n_{0} = 10^{29}\) m-3 and \(n_{0} = 10^{31}\) m-3.
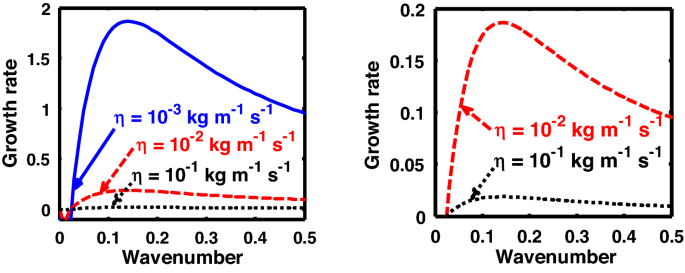
Same as Fig. 6, but for different values of the normalized kinematic viscosity \(\left( {\eta^{*} } \right)\). The second subplot is the enlarged version clearly highlighting the trends for \(\eta = 10^{ – 2}\) kg m-1 s-1 and \(\eta = 10^{ – 1}\) kg m-1 s-1.
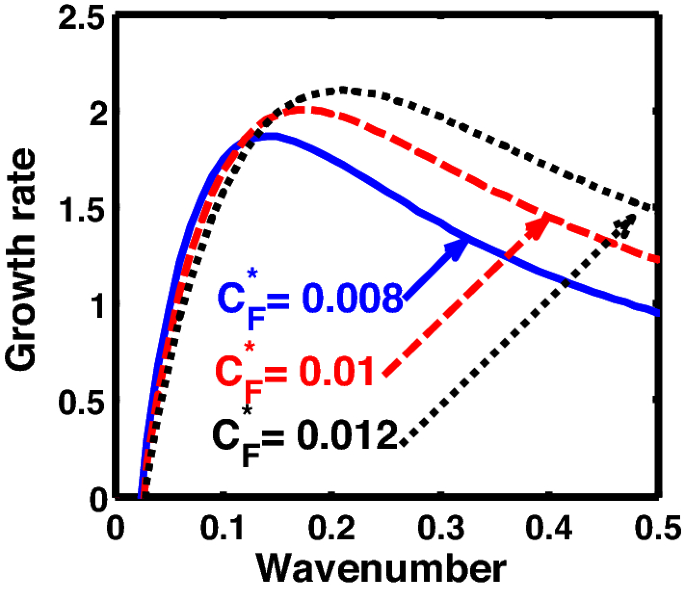
Same as Fig. 6, but for different values of the normalized Coriolis rotational force \(\left( {C_{F}^{*} } \right)\).
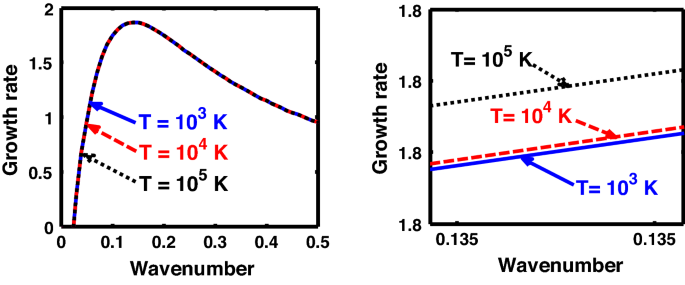
Same as Fig. 6, but for different values of the normalized thermal temperature \(\left( {T^{*} } \right)\). The second subplot is the magnified version depicting the peaks clearly.
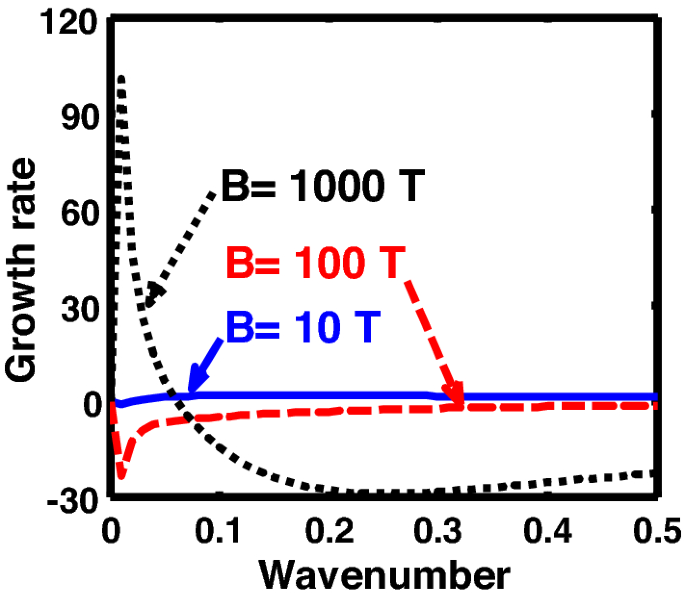
Same as Fig. 6, but for different values of the magnetic field \(\left( B \right)\).
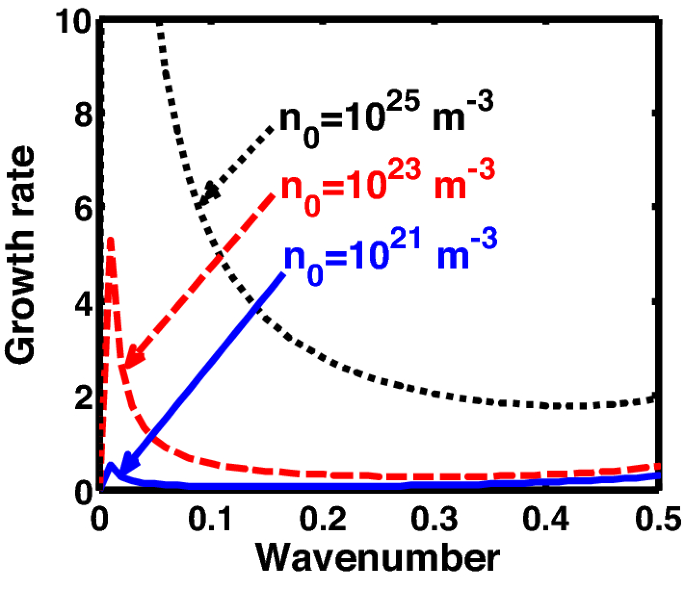
Profile of the normalized growth rate \(\left( {\Omega_{i} } \right)\) with variation in the normalized wavenumber \(\left( {k^{*} } \right)\). The different lines link to different values of the equilibrium number density \(\left( {n_{0} } \right)\) in non-planar (cylindrical) geometry in the classical regime (\(\hbar \to 0\)).
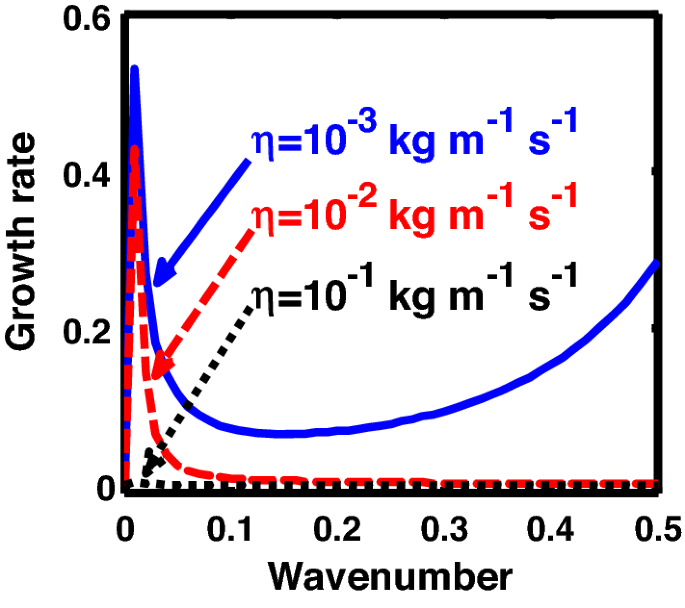
Same as Fig. 11, but for different values of the normalized kinematic viscosity \(\left( {\eta^{*} } \right)\).
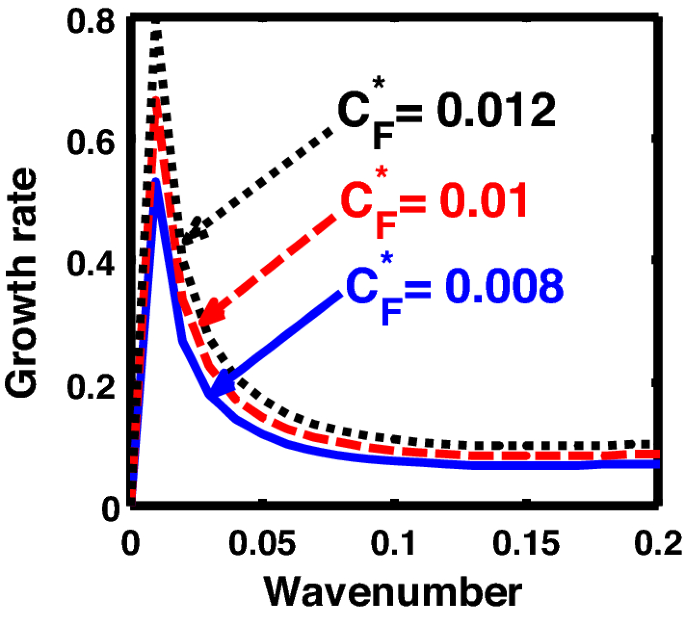
Same as Fig. 11, but for different values of the normalized Coriolis rotational force \(\left( {C_{F}^{*} } \right)\).
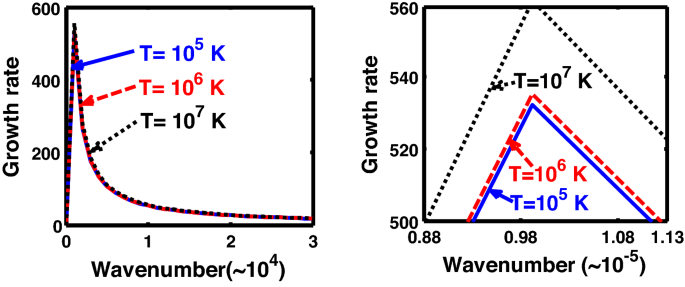
Same as Fig. 11, but for different values of the normalized thermal temperature \(\left( {T^{*} } \right)\). The second subplot is the magnified version depicting the peaks (kinks) clearly.
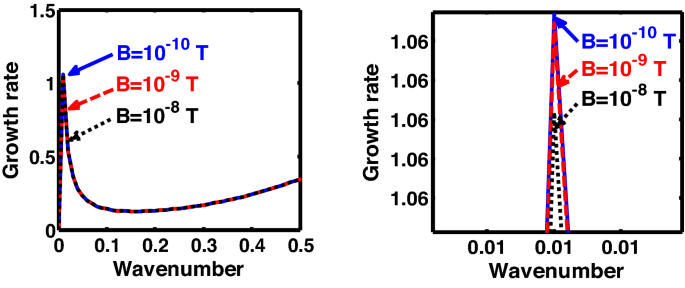
Same as Fig. 11, but for different values of the magnetic field \(\left( B \right)\). The second subplot is the magnified version depicting the peaks (kinks) clearly.
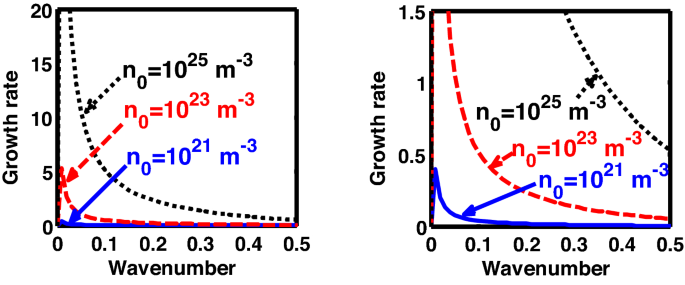
Profile of the normalized growth rate \(\left( {\Omega_{i} } \right)\) with variation in the normalized wavenumber \(\left( {k^{*} } \right)\). The different lines link to different values of the equilibrium number density \(\left( {n_{0} } \right)\) in planar (non-cylindrical) geometry in the classical regime (\(\hbar \to 0\)). The second subplot is its enlarged version clearly showing the trends for \(n_{0} = 10^{21}\) m-3 and \(n_{0} = 10^{23}\) m-3.
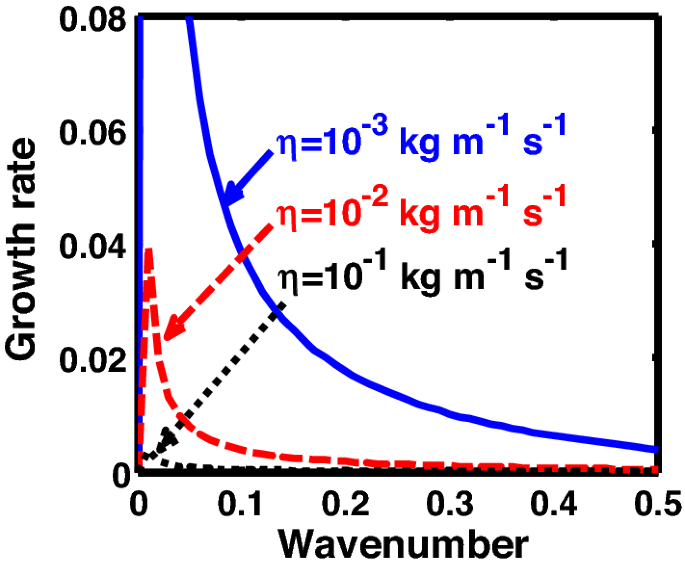
Same as Fig. 16, but for different values of the normalized kinematic viscosity \(\left( {\eta^{*} } \right)\).
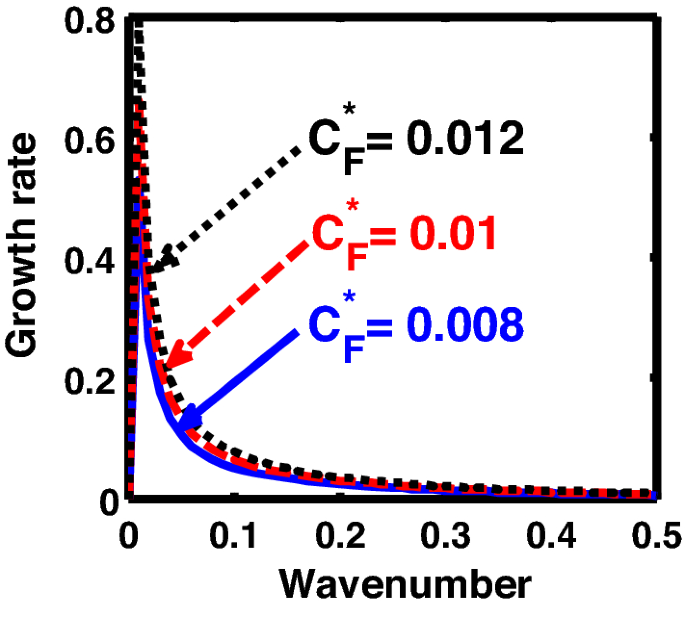
Same as Fig. 16, but for different values of the normalized Coriolis rotational force \(\left( {C_{F}^{*} } \right)\).
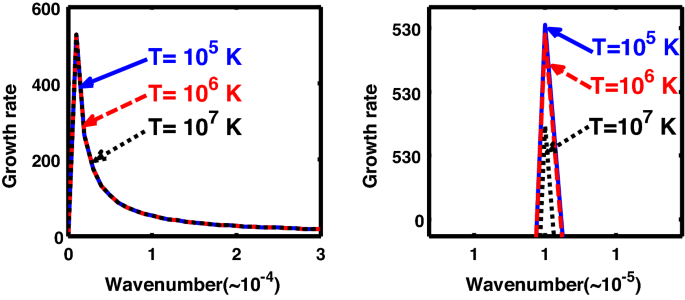
Same as Fig. 16, but for different values of the normalized thermal temperature \(\left( {T^{*} } \right)\). The second subplot is the magnified version depicting the peaks (kinks) clearly.
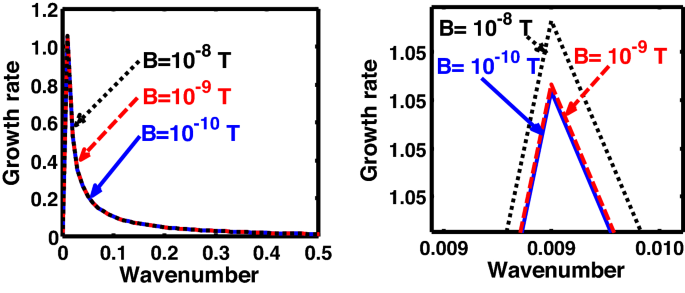
Same as Fig. 16, but for different values of the magnetic field \(\left( B \right)\). The second subplot is the magnified version depicting the peaks (kinks) clearly.
Thus, it is clearly seen that, in all the four considered distinct regimes, the modified dispersion relation has sensitive dependencies on the multiparametric model coefficients influencing the stability dynamics of the considered plasma system.



 Bitcoin
Bitcoin  Ethereum
Ethereum  Tether
Tether  XRP
XRP  USDC
USDC  TRON
TRON  Lido Staked Ether
Lido Staked Ether  Dogecoin
Dogecoin  Figure Heloc
Figure Heloc  Cardano
Cardano  WhiteBIT Coin
WhiteBIT Coin  Wrapped stETH
Wrapped stETH  Bitcoin Cash
Bitcoin Cash  Wrapped Bitcoin
Wrapped Bitcoin  USDS
USDS  Wrapped eETH
Wrapped eETH  Chainlink
Chainlink  Binance Bridged USDT (BNB Smart Chain)
Binance Bridged USDT (BNB Smart Chain)  Monero
Monero  WETH
WETH  LEO Token
LEO Token  Zcash
Zcash  Stellar
Stellar  Hyperliquid
Hyperliquid  Coinbase Wrapped BTC
Coinbase Wrapped BTC  Ethena USDe
Ethena USDe  Litecoin
Litecoin  Sui
Sui  Avalanche
Avalanche  Hedera
Hedera  sUSDS
sUSDS  Shiba Inu
Shiba Inu  USDT0
USDT0  Dai
Dai  Uniswap
Uniswap  PayPal USD
PayPal USD  Mantle
Mantle  Cronos
Cronos  World Liberty Financial
World Liberty Financial  Toncoin
Toncoin  Ethena Staked USDe
Ethena Staked USDe  Canton
Canton  Polkadot
Polkadot  USD1
USD1  Rain
Rain  Bitget Token
Bitget Token  MemeCore
MemeCore  Aave
Aave