The possibility of bound states is determined by the boundary conditions at \(x = 0\). Let the solution for \(x < 0\) that vanishes at infinity be \(\psi_{{\text{L}}} = (\psi_{{{\text{1L}}}} ,\psi_{{{\text{2L}}}} )\) and it be proportional to a constant, say \(C_{3}\). Then the continuity condition of the wave function:
$$\left. {\psi_{{{\text{1L}}}} } \right|_{x \to – 0} = \left. {\psi_{{{\text{1R}}}} } \right|_{x \to + 0} ,$$
(22)
$$\left. {\psi_{{{\text{2L}}}} } \right|_{x \to – 0} = \left. {\psi_{{{\text{2R}}}} } \right|_{x \to + 0} ,$$
(23)
presents a set of two homogeneous linear equations with respect to the constants \(C_{1}\) and \(C_{3}\). For a non-trivial solution, the determinant of this system must be zero:
$$\left. {\psi_{{{\text{1L}}}} } \right|_{x \to – 0} \left. {\psi_{{{\text{2R}}}} } \right|_{x \to + 0} – \left. {\psi_{{{\text{1R}}}} } \right|_{x \to + 0} \left. {\psi_{{{\text{2L}}}} } \right|_{x \to – 0} = 0.$$
(24)
Since we consider the odd extension, when \(W\left( { – x} \right) = – W\left( x \right)\), the Dirac equation is covariant under the parity transformation \(x \to \,- x\), and the solution for the negative \(x\)-region can be written as \(\psi_{{\text{L}}} (x) = C_{3} \left( {\psi_{{{\text{1R}}}} ( – x), – \psi_{{{\text{2R}}}} ( – x)} \right)\). As a result, Eq. (24) reduces to \(\psi_{{1{\text{R}}}} \left( 0 \right)\psi_{{2{\text{R}}}} \left( 0 \right) = 0\), and we obtain two branches of bound states, generated by \(\psi_{{1{\text{R}}}} \left( 0 \right) = 0\) or \(\psi_{{2{\text{R}}}} \left( 0 \right) = 0\). Let us consider these cases separately.
Bound states with \(\psi_{{1{\text{R}}}} \left( 0 \right) = 0\)
The equation for the bound states’ energy spectrum is
$$F\left( E \right) = 2\left( {a – 1} \right)H_{a – 2} (y_{0} ) + \left( {b_{0} – 2y_{0} } \right)H_{a – 1} (y_{0} ) = 0,\quad y_{0} = \frac{{4W_{0} W_{1} }}{{c^{2} \hbar^{2} \delta^{3/2} }}.$$
(25)
The behavior of \(F\) as a function of energy is shown in Fig. 3.
The behavior of function \(F(E)\) of Eq. (25) in the negative (left panel) and positive (right panel) energy regions. The points show the position of \(\varepsilon = \pm mc^{2}\). The roots are all located in the intervals \(\left( { – \sqrt {m^{2} c^{4} + W_{0}^{2} } , – mc^{2} } \right)\) and \(\left( {mc^{2} ,\sqrt {m^{2} c^{4} + W_{0}^{2} } } \right)\). \(f = 2^{a/2} e^{{y_{0}^{2} /2}} \sqrt {(a + 1)!} ,\quad \left( {m,c,\hbar ,W_{1} ,W_{2} } \right) = \left( {1,1,1, – 1/2,1} \right)\).
It can be shown that, provided \(W_{0} W_{1} < 0\), the spectrum equation has infinitely many roots, all located in the intervals
$$E \in \left( { – \sqrt {m^{2} c^{4} + W_{0}^{2} } , – mc^{2} } \right)\quad and\quad E \in \left( {mc^{2} ,\sqrt {m^{2} c^{4} + W_{0}^{2} } } \right).$$
(26)
To construct an approximation for the spectrum, it is convenient to transform Eq. (25), using the recurrence relations between contiguous Hermite functions40, into the form
$$\frac{{2ay_{0} + b_{0} \left( {a + 1 – 2y_{0}^{2} } \right)}}{{b_{0} y_{0} – a}}H_{a + 1} (y_{0} ) + H_{a + 2} (y_{0} ) = 0.$$
(27)
The advantage of this form is that the argument \(y_{0}\) of the involved Hermite functions here is such that it belongs to the left transient region \(y_{0} \approx \sqrt {2\nu – 1}\), where \(\nu = a + 1\) or \(\nu = a + 2\). Then, using the Airy-function approximation of the Hermite function for this region41, we arrive at an approximation of this equation as
$$\sin \left( {\pi a – \frac{{A_{0} \left( {E_{0} – E} \right) + A_{1} \left( {E – mc^{2} } \right)}}{{E_{0} – mc^{2} }}} \right) = 0,$$
(28)
where
$$E_{0} = \sqrt {m^{2} c^{4} + W_{0}^{2} } ,$$
(29)
$$A_{0} = \frac{\pi }{2} – \tan^{ – 1} \left( {\frac{{Ai\left( {2^{1/3} 3^{1/6} \left( {\sqrt 2 u^{3/4} – \sqrt 3 } \right)} \right)}}{{Bi\left( {2^{1/3} 3^{1/6} \left( {\sqrt 2 u^{3/4} – \sqrt 3 } \right)} \right)}}} \right),$$
(30)
$$A_{1} = \frac{\pi }{2} – \tan^{ – 1} \left( {\frac{{Ai^{\prime } \left( u \right) – \sqrt u Ai\left( u \right)}}{{Bi^{\prime } \left( u \right) – \sqrt u Bi\left( u \right)}}} \right),$$
(31)
$${\text{and}}\quad u = \frac{{W_{1}^{4/3} }}{{\left( { – W_{0} c\hbar } \right)^{2/3} }}.$$
(32)
It is shown that \(A_{0,1} < 1\) and for the solution of Eq. (29), \(a > 1\). Furthermore, for large \(a\), the energy \(E\) is close to \(E_{0}\): \(E \approx E_{0}\). With these observations, for large a, we arrive at the approximate equation
$$\pi a – A_{1} = \pi n,\,\,\,\,\,n = 1,2,3,….$$
(33)
The dependence of \(a\) on \(E\) (see Eq. (19)) shows that this is a sextic polynomial equation in \(E\) that is readily reduced to a cubic one. The real roots of the equation are given as
$$E_{n} = \pm \sqrt {m^{2} c^{4} + \left( {1 – e_{n} } \right)W_{0}^{2} } ,$$
(34)
where, using Cardano’s formula for the cubic,
$$\begin{gathered} e_{n} = \frac{1}{3b} + \frac{{2^{1/3} \left( {6b – 1} \right)}}{{3b\left( {18b – 2 – 27b^{2} + 3\sqrt {b^{3} \left( {81b – 12} \right)} } \right)^{1/3} }} – \\ \frac{{2^{ – 1/3} }}{3b}\left( {18b – 2 – 27b^{2} + 3\sqrt {b^{3} \left( {81b – 12} \right)} } \right)^{1/3} \\ \end{gathered}$$
(35)
$${\text{and}}\quad b = \left( {\frac{{c\hbar W_{0} }}{{W_{1}^{2} }}} \right)^{2} \left( {n – 1 + \frac{{A_{1} }}{\pi }} \right)^{2} .$$
(36)
This is a fairly accurate approximation. It provides the spectrum with relative error of the order of \(10^{ – 4}\) or less (see Table 1 for a comparison with the exact numerical result). The normalized wave function on the entire \(x\)-axis is shown in Fig. 4 (\(n = 3\), positive energy branch). It can be observed that the wave function is anti-symmetric with respect to the origin, as expected, and that the derivative of \(\psi_{2} (x)\) is discontinuous at the origin.
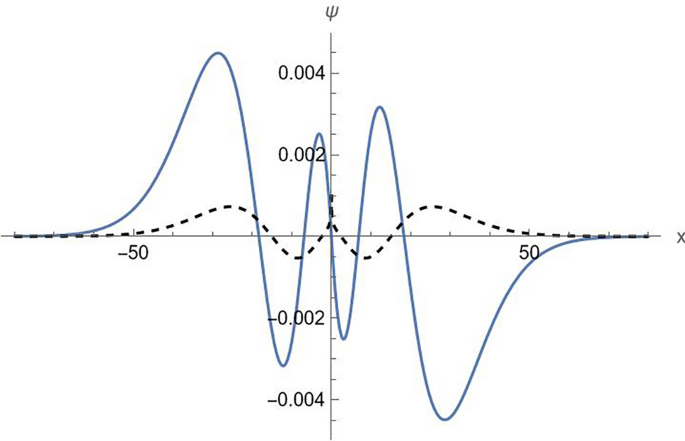
Normalized wave function with \(\psi_{1} (0) = 0\) (\(n = 3\), \(E_{3} = 1.053641\)). The solid line shows \(\psi_{1}\) and the dashed line shows \(\psi_{2} /i\). \(\left( {m,c,\hbar ,W_{1} ,W_{2} } \right) = \left( {1,1,1, – 1/2,1} \right)\).
Bound states with \(\psi_{{{\text{2R}}}} \left( 0 \right) = 0\)
This time, the exact spectrum equation is written as
$$g\,H_{a + 1} (y_{0} ) + H_{a + 2} (y_{0} ) = 0,$$
(37)
$$g = \frac{{4\left( {2W_{1}^{2} – c^{2} \hbar^{2} \delta } \right)\left( {m^{2} c^{4} + W_{0}^{2} – E^{2} } \right) – 8W_{0} W_{1}^{2} \left( {c\hbar \delta – W_{0} } \right)}}{{W_{1} c^{2} \hbar^{2} \delta^{3/2} \left( {c\hbar \delta – 2W_{0} } \right)}},$$
(38)
Acting now essentially in the same way as in the previous case, we arrive at the spectrum expressed by the same formulas (34)–(36), with the parameter \(A_{1}\) given as
$$A_{1} = – \tan^{ – 1} \left( {\frac{{\sqrt u Ai\left( u \right) + Ai^{\prime } \left( u \right)}}{{\sqrt u Bi\left( u \right) + Bi^{\prime } \left( u \right)}}} \right),$$
(39)
where \(u\) is given by Eq. (32). The obtained result again is a fairly good approximation as seen from Table 2. The normalized wave function on the entire \(x\)-axis is shown in Fig. 5 (\(n = 3\), positive energy branch). It can be observed that this time the derivative of \(\psi_{1} (x)\) is discontinuous at the origin.
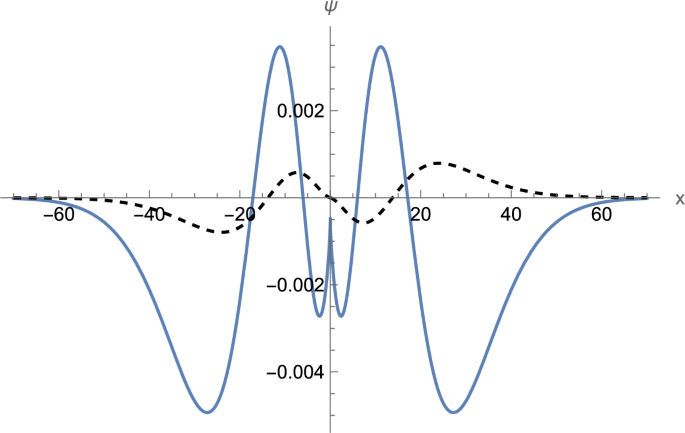
Normalized wave function with \(\psi_{2} (0) = 0\) (\(n = 3\), \(E_{3} = 1.052395\)). The solid line shows \(\psi_{1}\) and the dashed line shows \(\psi_{2} /i\). \(\left( {m,c,\hbar ,W_{1} ,W_{2} } \right) = \left( {1,1,1, – 1/2,1} \right)\).
As Eq. (36) shows, the Maslov index is given as
$$\gamma = – 1 + \frac{{A_{1} }}{\pi },$$
(40)
where the parameter \(A_{1}\) is different for the spectrum branches with \(\psi_{1} (0) = 0\) and \(\psi_{2} (0) = 0\). An interesting observation is that \(A_{1}\) is not a constant but depends on the potential parameters \(W_{0}\) and \(W_{1}\). Figure 6 shows this dependence. As we can see, the Maslov index for the energy spectrum branch with \(\psi_{1} (0) = 0\) starts from \(- 1/6\), while that for the branch with \(\psi_{2} (0) = 0\) starts from \(- 5/6\) as \(u = 0\). We note that both indices tend to \(- 1\) as \(u \to \infty\).
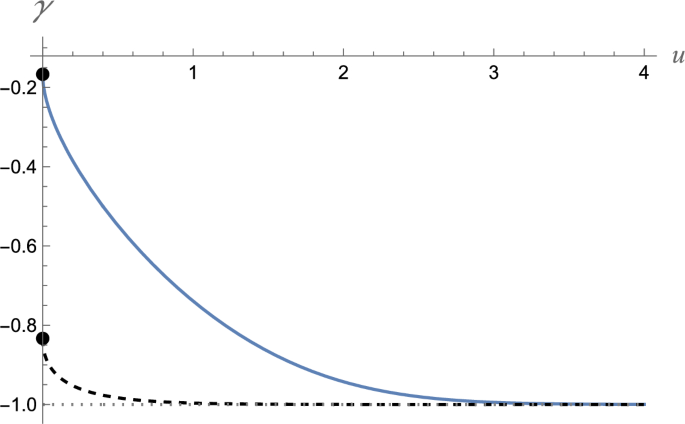
The dependence of the Maslov index on the parameter \(u = W_{1}^{4/3} /\left( { – W_{0} c\hbar } \right)^{2/3}\). The solid line shows the index for the energy spectrum branch with \(\psi_{1} (0) = 0\) and the dotted line stands for the branch with \(\psi_{2} (0) = 0\). The points in the vertical axis indicate \(- 1/6\) and \(- 5/6\).



 Bitcoin
Bitcoin  Ethereum
Ethereum  Tether
Tether  XRP
XRP  USDC
USDC  Lido Staked Ether
Lido Staked Ether  TRON
TRON  Dogecoin
Dogecoin  Figure Heloc
Figure Heloc  Cardano
Cardano  Bitcoin Cash
Bitcoin Cash  WhiteBIT Coin
WhiteBIT Coin  Wrapped stETH
Wrapped stETH  Wrapped Bitcoin
Wrapped Bitcoin  Wrapped eETH
Wrapped eETH  Chainlink
Chainlink  USDS
USDS  Binance Bridged USDT (BNB Smart Chain)
Binance Bridged USDT (BNB Smart Chain)  LEO Token
LEO Token  WETH
WETH  Zcash
Zcash  Monero
Monero  Stellar
Stellar  Coinbase Wrapped BTC
Coinbase Wrapped BTC  Ethena USDe
Ethena USDe  Litecoin
Litecoin  Sui
Sui  Hyperliquid
Hyperliquid  Avalanche
Avalanche  Canton
Canton  Hedera
Hedera  Shiba Inu
Shiba Inu  USDT0
USDT0  Toncoin
Toncoin  Dai
Dai  World Liberty Financial
World Liberty Financial  sUSDS
sUSDS  Uniswap
Uniswap  Cronos
Cronos  PayPal USD
PayPal USD  Ethena Staked USDe
Ethena Staked USDe  Polkadot
Polkadot  USD1
USD1  Mantle
Mantle  Rain
Rain  MemeCore
MemeCore  Pepe
Pepe  Bitget Token
Bitget Token