Theoretical studies of magneto-optical Kerr and Faraday effects in two-dimensional second-order topological insulators

Here we show numerical results of optical conductivities, Kerr and Faraday angles and ellipticity for 2D chiral SOTI in the presence of out-of-plane magnetization. In the absence of magnetization, model Hamiltonian (1) describes a second-order topological phase (\(\nu =1\))^9,13,47,48 when \(0<M<8B\) and a topologically trivial phase (\(\nu =0\)) otherwise. An introduction of magnetization may affect the topological behaviors of the system, thereby inducing a Chern insulating phase^49,50. The energy dispersions of Hamiltonian (1) are given by

with the band index \(\mu =1,2,3,4\). The bulk band gap between two middle bands closes at the high-symmetry momentum \(\Gamma =(0,0)\) when \(g=|M|\); at \(M=(\pi ,\pi )\) when \(g=|M-8B|\); at \(X=(\pi ,0)\) and \(Y=(0,\pi )\) when \(g=\sqrt{(M-4B)^2+4\varLambda ^2}\). As a result, diverse topological phases with different Chern number C can be realized by tuning the parameters. The phase diagrams of model Hamiltonian (1) are shown in Fig. 2, where both the Chern number C and second-order topological invariant \(\nu\) are provided. For different regimes of parameters, the phase diagrams can be quite different. To make the discussion explicit, we mainly focus on two regimes of parameters: weak and strong magnetization case, corresponding to case (a) and (e) of Fig. 2.

A. Weak magnetization. First we consider the case with weak magnetization, corresponding to Fig. 2a. In this case, \(X=(\pi ,0)\) and \(Y=(0,\pi )\) are no longer gap closing points for any given parameters. As a result, the Chern number becomes \(C=1\) when \(-g< M < g\) or \(8B-g< M < 8B+g\), and \(C=0\) otherwise. To check the topological properties, we plot the energy spectrum and wave function distribution of finite-size samples in Fig. 3 for parameters: \(M/t=1\), 0 and \(-1\) with \(B/t=0.25\). In the absence of magnetization, these parameters correspond to the SOTI, semimetal and trivial phase, respectively. When magnetization is induced, according to Fig. 2a, these parameters correspond to the SOTI, Chern insulating and trivial phase, respectively. In Fig. 3a and b, we can see the existence of zero-energy corner states. In Fig. 3c and d, we can see the existence of gapless edge states. Such real-space calculations prove our results of phase diagram.

The band dispersions along the high-symmetry lines of Brillouin zone are shown in Fig. 4. Different values of M are considered, and Chern numbers are also labeled. Note that the model shows symmetric behaviors between parameters \(M>4B\) and \(M<4B\), thus we only choose parameters with \(M\le 4B\), including \(M/t=1\), 0 and \(-1\). \(T_i\) (\(T_o\)) labels the optical transitions for two inner (outer) branches of bands. Remarkably, there are new crossings in both conduction and valence bands of SOTI in the \(\Gamma -M\) direction (see Fig. 4a), which are absent in the trivial phase. The topological protection of band crossings can be understood by noting that in the \(\Gamma -M\) direction (i.e., \(k_x=k_y\)), \(H_{\varLambda }(\varvec{k})=0\) for Hamiltonian (1). Thus the model reduces to that of topological insulators. For topological insulating phase (\(0<M<8B\)), the bands are inverted at the \(\Gamma\) or M point, leading to the band crossings between them. For trivial phase, there are no band inversions or crossings.

Related articles

BlockDAG’s CEO and Team Announced: Expected to Surpass Hedera and Polygon with a $1 Projection

30 July 2024

VeChain (VET) And Hedera (HBAR) Triple Red Charts. Rollblock (RBLK) Seems The Summer Sure Money Bet – Times Tabloid

28 July 2024

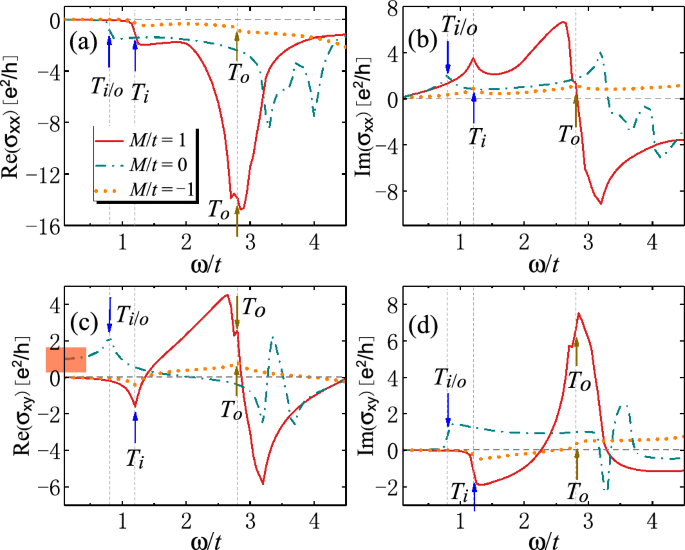
Real and imaginary part of optical conductivities (a–b) \(\sigma _{xx}\) and (c–d) \(\sigma _{xy}\) (in units of \(e^2/h\)) as functions of photon energy \(\omega\) (in units of t) for 2D SOTI with weak magnetization. The arrows label the energies of optically-induced inner (outer) interband transitions \(T_i\) (\(T_o\)). The universal value of \(\textrm{Re}[\sigma _{xy}]\) in the low-energy limit is highlighted in red in (c). Parameters: \(t=0.06\) eV⁴³, \(B/t=0.25\), \(\varLambda /t=1.0\), \(g/t=0.4\), \(\epsilon _r=4\)^31,45, \(\mu _r=1\), \(\hbar /\tau _s=0.05\), \(E_F=0\).

The real and imaginary part of optical conductivities \(\sigma _{xx}\) and \(\sigma _{xy}\) are plotted in Fig. 5, where for convenience we set the Fermi energy \(E_F=0\). A striking difference between SOTI (\(M/t=1\)) and trivial insulators (\(M/t=-1\)) lies in their order of magnitude. In SOTI, \(\sigma _{xx}\) and \(\sigma _{xy}\) are enhanced due to the existence of additional channels of interband transitions. Threshold photon energies for the interband transitions \(T_{i}\) and \(T_o\) are indicated by arrows in Fig. 5. At these transitions, \(\textrm{Re}[\sigma _{xx}]\) and \(\textrm{Im}[\sigma _{xy}]\) show sudden jumps while \(\textrm{Re}[\sigma _{xy}]\) and \(\textrm{Im}[\sigma _{xx}]\) show positive or negative peaks. For example, in Fig. 5a, \(\textrm{Re}[\sigma _{xx}]\) show sudden jumps for \(M/t=\pm 1\) at \(\omega /t=1.2\) due to the activation of inner interband transitions \(T_i\). At \(\omega /t=2.8\), another jumps occur due to the activation of outer interband transitions \(T_o\). For moderate photon energy \(\omega\), the magnitude of \(\textrm{Re}[\sigma _{xx}]\) for SOTI (\(M/t=1\)) becomes much larger than trivial insulators (\(M/t=-1\)). This is attributed to the crossing points along the \(\Gamma M\) line of the Brillouin zone of SOTI (see Fig. 4a), which induces new channels of interband transitions at some non-high-symmetry momentum along the \(\Gamma M\) line. Moreover, the states at the high-symmetry point \(M=(\pi ,\pi )\) have non-negligible contributions due to the band degeneracy between \(\Gamma\) and M. These together contribute to the large magnitude of \(\textrm{Re}[\sigma _{xx}]\) in SOTI. Similar arguments can be given to \(\textrm{Im}[\sigma _{xy}]\) (see Fig. 5d). On the other hand, \(\textrm{Im}[\sigma _{xx}]\) and \(\textrm{Re}[\sigma _{xy}]\) are proportional to the slope of \(\textrm{Re}[\sigma _{xx}]\) and \(\textrm{Im}[\sigma _{xy}]\), respectively, thereby exhibiting giant jumps near the small peaks at \(\omega /t=2.8\) (see Fig. 5b and c). At even higher photon energy, the magnitude of \(\sigma _{xx}\) and \(\sigma _{xy}\) is greatly reduced due to the closure of optical interband transitions.

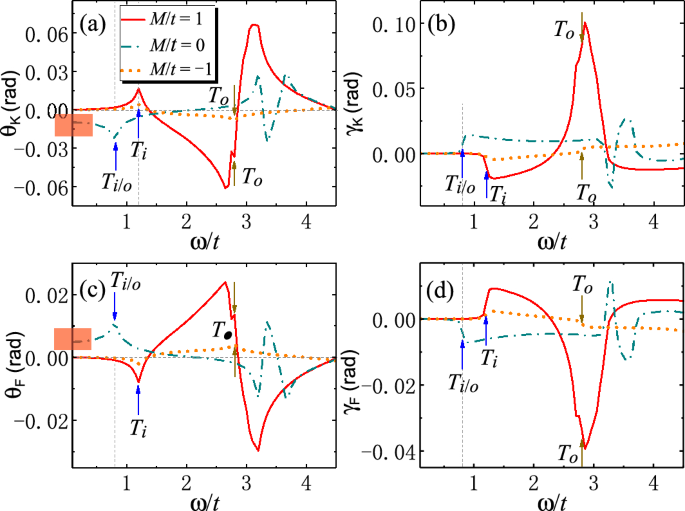
(a) Kerr and (c) Faraday angles and (b) Kerr and (d) Faraday ellipticity as functions of photon energy \(\omega\) (in units of t) for 2D SOTI. The arrows label the energies of optically-induced inner (outer) interband transitions \(T_i\) (\(T_o\)). The universal values of \(\theta _K\) and \(\theta _F\) in the low-energy limit are highlighted in red in (a) and (c). Parameters: \(t=0.06\) eV⁴³, \(B/t=0.25\), \(\varLambda /t=1.0\), \(g/t=0.4\), \(\epsilon _r=4\)^31,45, \(\mu _r=1\), \(\hbar /\tau _s=0.05\), \(E_F=0\).

According to Eq. (8), the conditions for the occurrence of crossing points are given by \(m(\varvec{k})=\varLambda (\varvec{k})=0\). That is, \(k_x=k_y\) (\(\Gamma M\) line) and \(M-4B[1-\cos (k_{x})]=0\). The critical values of parameters are \(M=0\) and \(M=8B\), which exactly agree with the parameter range for SOTI. This means that the large magnitude of \(\textrm{Re}[\sigma _{xx}]\), \(\textrm{Im}[\sigma _{xy}]\) and the giant jump of \(\textrm{Im}[\sigma _{xx}]\), \(\textrm{Re}[\sigma _{xy}]\) may potentially be used to characterize the SOTI phase. However, such argument is not applicable for the critical value \(M=0\), in which case the magnetization drives the system into Chern insulators with Chern number \(C=1\) (see Fig. 4b). In this situation, the Chern insulating phase can be distinguished by the integer Hall conductivity in the low-energy limit, that is, \(\textrm{Re}[\sigma _{xy}]=e^2/h\) as highlighted in Fig. 5c.

ADVERTISEMENT

The Kerr and Faraday angles \(\theta _K\), \(\theta _F\) and ellipticity \(\gamma _K\), \(\gamma _F\) are plotted in Fig. 6. It is manifest that \(\theta _K\) and \(\theta _F\) (also \(\gamma _K\) and \(\gamma _F\)) are complementary to each other. Basically, \(\theta _F\) (\(\theta _K\)) shows the same (opposite) behaviors as \(\textrm{Re}[\sigma _{xy}]\) in Fig. 5c. This can be understood from Eq. (5), where \(Z_0\sigma _{\pm }\ll 1\) can be treated as perturbations. After some algebra, we have \(\theta _F\propto -\theta _K\propto \textrm{Re}[\sigma _{xy}]\). This means that Kerr and Faraday angles inherit the properties from Hall conductivity \(\textrm{Re}[\sigma _{xy}]\), and hence can also be used to characterize the SOTI. \(\gamma _K\) and \(\gamma _F\) seem more likely to inherit the properties from \(\textrm{Im}[\sigma _{xy}]\), which, together with the Kerr and Faraday angles, can be adopted to distinguish SOTI from trivial insulators.

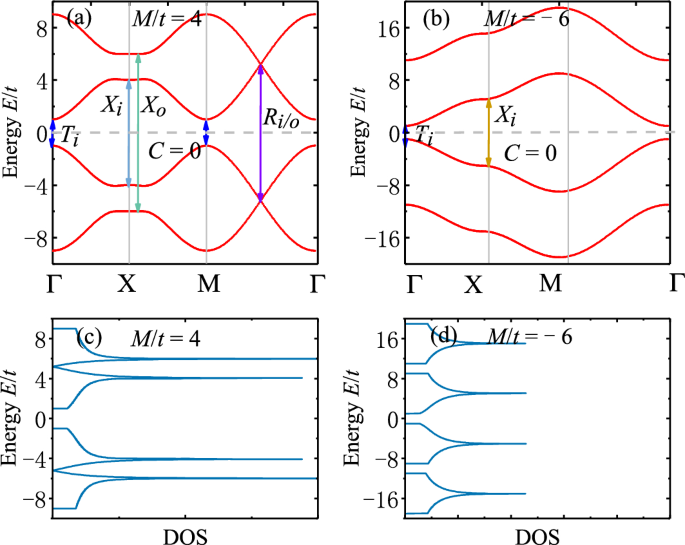
Band dispersions and density of states (DOS) of 2D second-order topological insulators (SOTI) with strong magnetization for parameters (a), (c) \(M/t=4\) and (b), (d) \(M/t=-6\). The optically-induced inner (outer) interband transitions \(T_{i/o}\) at \(\Gamma\), \(X_{i/o}\) at X and \(R_{i/o}\) at the crossing points are depicted by double arrows. In the absence of magnetization, \(M/t=4\) and \(-6\) correspond to SOTI and trivial insulator, respectively. In the presence of magnetization, the Chern number in each case is indicated. Parameters: \(t=0.06\) eV⁴³, \(B/t=1\), \(\varLambda /t=0.5\), \(g/t=5\).

B. Strong magnetization. Now we consider the case with strong magnetization, corresponding to Fig. 2e. We consider two representative parameters: \(M/t=4\) and \(M/t=-6\). In the absence of magnetization, they correspond to the SOTI and trivial phase, respectively. When strong magnetization is induced, the band structure is modified greatly, and \(M/t=4\) now reduces to trivial insulating phase. However, we reveal in the following that \(M/t=4\) and \(M/t=-6\) have distinct optical features as they originate from different topological phases in the absence of magnetization.

The band dispersions along the high-symmetry lines of Brillouin zone are shown in Fig. 7, where two representative parameters are considered: \(M/t=4\) (SOTI) and \(M/t=-6\) (trivial). We find that similar to the case with weak magnetization, there are crossings in both conduction and valence bands of SOTI, which are absent for trivial phase. The threshold optical transitions for two inner (outer) branches of bands are labeled as \(T_{i/o}\) at \(\Gamma\) point, \(X_{i/o}\) at X and \(R_{i/o}\) at the crossing points. At the \(\Gamma\) or M point of Brillouin zone, transitions \(T_{i/o}\) are allowed since the initial and final states share the same spin angular momentum. At the X point, \(H_{\varLambda }(\varvec{k})\) from Eq. (1) mixes states with different spins, despite the fact that inner and outer states are orthogonal to each other. As a result, only transitions \(X_{i/o}\) within inner or outer states are allowed.

The optical conductivities \(\sigma _{xx}\) and \(\sigma _{xy}\) are plotted in Fig. 8, where the interband transitions contributing to the peaks and jumps are indicated by arrows. We find that SOTI show larger peaks of \(\textrm{Re}[\sigma _{xx}]\) and jumps of \(\textrm{Im}[\sigma _{xx}]\) from optical transitions \(R_{i/o}\) than trivial insulators. Nevertheless, their differences are much smaller than those in the weak-magnetization case. This is due to the loss of degenerate channels of optical transitions driven by strong magnetization. On the other hand, strong magnetization induces nearly flat bands at X point for SOTI (see Fig. 7a), which still gives rise to giant peaks and jumps of optical conductivities as a result of the enhanced joint density of states for optical transitions \(X_{i/o}\) (see Fig. 7c). This may provide another way to distinguish SOTI from trivial insulators.

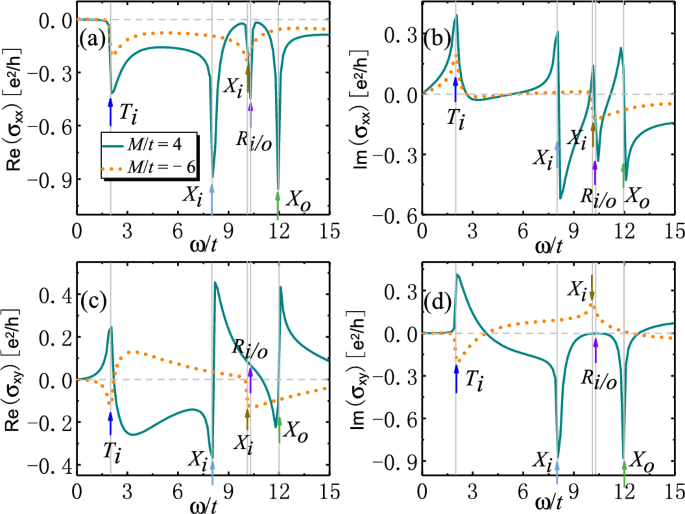
Real and imaginary part of optical conductivities (a–b) \(\sigma _{xx}\) and (c–d) \(\sigma _{xy}\) (in units of \(e^2/h\)) as functions of photon energy \(\omega\) (in units of t) for 2D SOTI with strong magnetization. The arrows label the energies of optically-induced inner (outer) interband transitions \(T_{i/o}\), \(X_{i/o}\) and \(R_{i/o}\). Parameters: \(t=0.06\) eV⁴³, \(B/t=1\), \(\varLambda /t=0.5\), \(g/t=5\), \(\epsilon _r=4\)^31,45, \(\mu _r=1\), \(\hbar /\tau _s=0.05\), \(E_F=0\).

The resulting Kerr and Faraday angles and ellipticities are plotted in Fig. 9. There are two successive giant jumps (peaks) in both \(\theta _K\) and \(\theta _F\) (\(\gamma _K\) and \(\gamma _F\)) originating from optical transitions \(X_{i/o}\) for SOTI. By contrast, there is only one small jump or peak from optical transitions \(X_{i}\) for trivial insulators. Compared with weak magnetization, strong magnetization tends to suppress the magnitude of Kerr and Faraday angles and ellipticity. The reduction of Kerr and Faraday angles and ellipticity is due to the enhancement of band gaps modified by strong magnetization. This leads to the suppression of optical Hall conductivities, thus the reduction of Kerr and Faraday rotations. This reduction under strong magnetization is different from the general view of magneto-optical effects due to strong magnetic field, where Landau levels are formed. Here the magnetization does not induce Landau levels, but just modifies the band structure. However, even for the reduced Kerr and Faraday angles and ellipticity, they are still within the experimental reach.

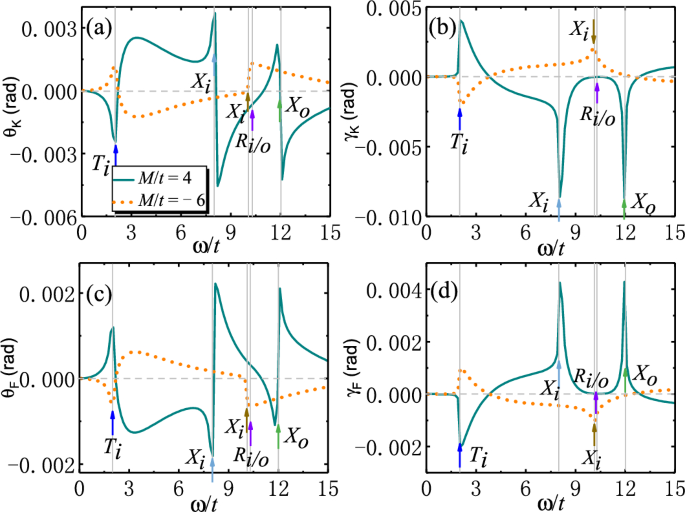
(a) Kerr and (c) Faraday angles and (b) Kerr and (d) Faraday ellipticity as functions of photon energy \(\omega\) (in units of t) for 2D SOTI with strong magnetization. The arrows label the energies of optically-induced inner (outer) interband transitions \(T_{i/o}\), \(X_{i/o}\) and \(R_{i/o}\). Parameters: \(t=0.06\) eV⁴³, \(B/t=1\), \(\varLambda /t=0.5\), \(g/t=5\), \(\epsilon _r=4\)^31,45, \(\mu _r=1\), \(\hbar /\tau _s=0.05\), \(E_F=0\).